はじめに
流体解析(Computed Fluid Dynamics:CFD)は、最適な攪拌条件を求める際に活用されています。この際、粒子等の固体材料を考慮した固液攪拌では、攪拌槽内の粒子の挙動を解くために個別要素法(Discrete Element Method:DEM)を加えた流体と粒子の連成解析(CFD-DEMカップリング)が必要となります。
本解析事例では、解析ソフト未経験者や導入を検討している方向けに、解析ソフトの活用例をイメージしてもらうため、固液攪拌の攪拌条件を調査してく様子を示します。
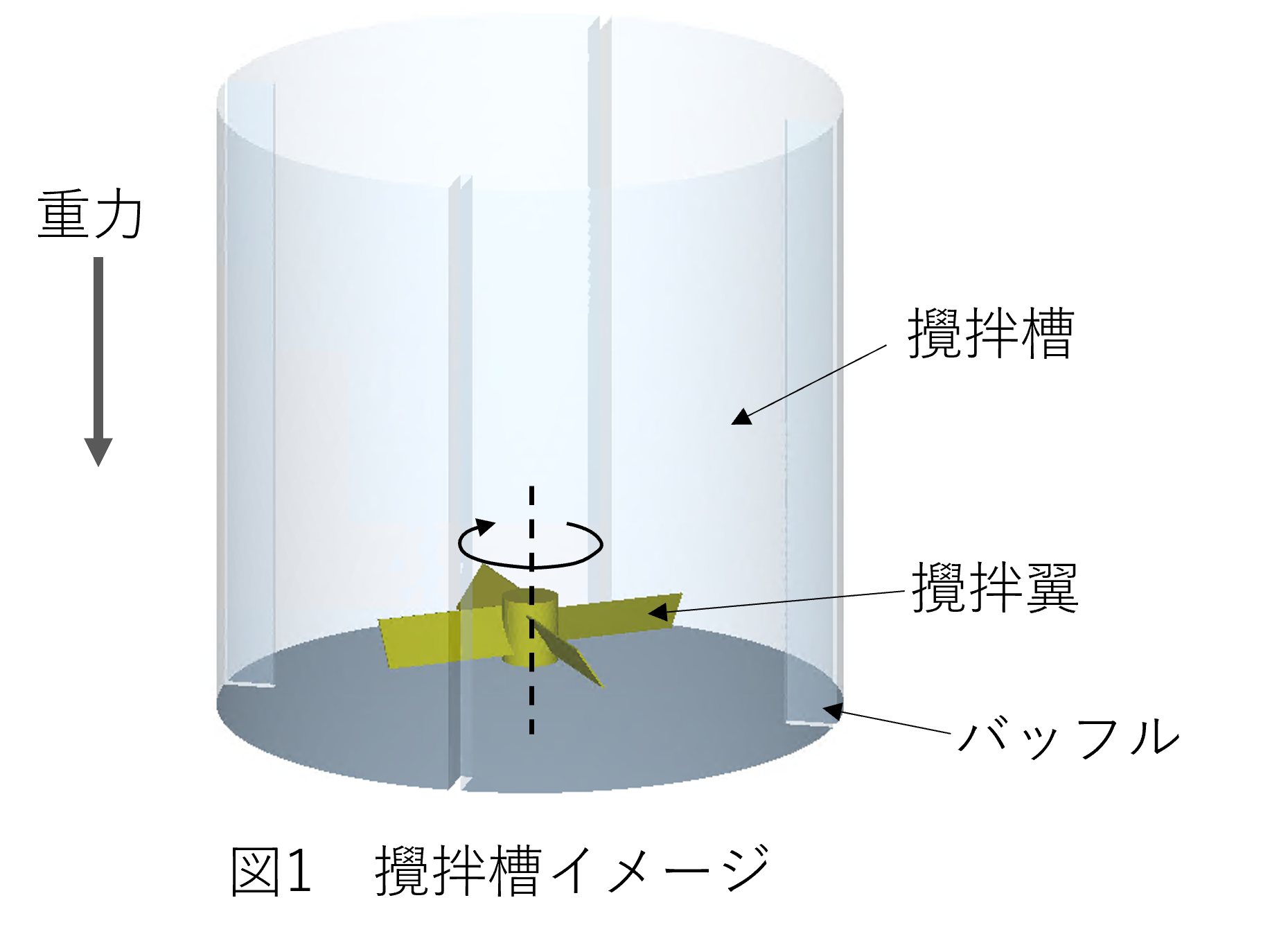
解析に使用したソフトはアルテア社の流体解析ソフトAcuSolveと個別要素法解析ソフトEDEMとし、図1に示す攪拌槽と攪拌翼で、バッフル形状を変更した計算を実施します。計算は、3次元-非定常-非圧縮とし、30秒間計算します。 なお、攪拌条件は以下の条件のもと調査します。
--- 制約条件 ----
・ 攪拌翼のトルク上限は4.0 N・mとする
・ 攪拌翼と攪拌槽の形状は変更しない
・ 液体や粒子の物性は変更しない
連成計算の設定
液体内の粒子は密度が異なる2種類存在していものとします。なお、実際の粒子径φは2~3 mmの間で分布を持っていますが、攪拌条件の検討が目的のため、最小(2 mm)と最大(3 mm)の粒子径のみ考慮して計算します。
なお、液相に対して粒子が占める体積は5%程度と小さいため、one-wayカップリングで計算します。抗力モデルはWen-Yu、揚力はSchiller-Naumanを適用して計算します。
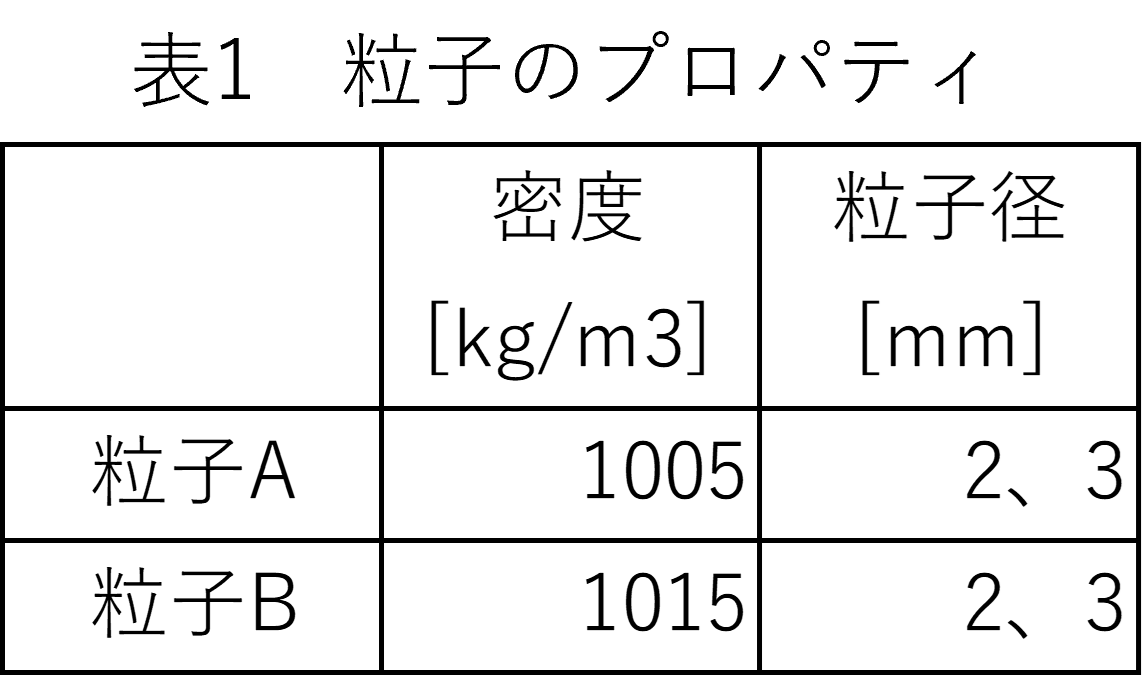

また、本モデルの攪拌レイノルズ数Rerotを計算すると6万程度でした。一般的にRerot < 50では層流、 50 < Rerot < 1000では遷移域、 Rerot > 1000では乱流と言われています。本モデルは乱流と判断できるため、RANSの1方程式モデルSpalart-Allmarasを適用して計算します。
検討1:確認計算
過去に実施してきた攪拌の経験から、液体だけ(固相無し)であれば、10 RPM程度で許容時間内に問題なく攪拌できていることがわかっているものとします。このため、初めに10 RPMで計算し、翼に作用するトルクと粒子の分散状況がどのようになるか確認計算を実施します。
なお、バッフルの存在により界面に渦はほぼ発生しないものとし、界面形状はフラットとみなしfree-slipで計算します。
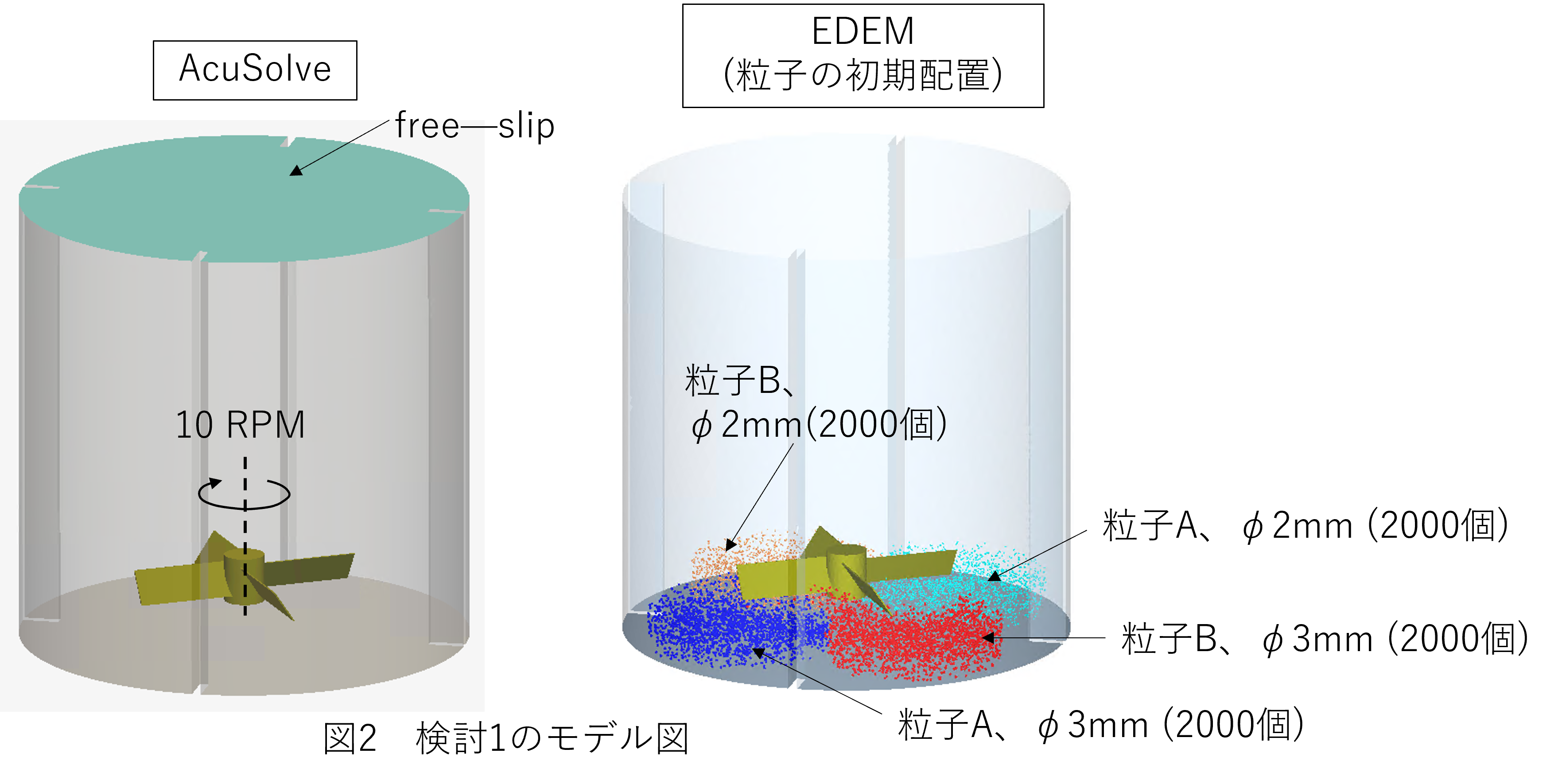

図3と図4に、各断面の流速分布と流速ベクトルを示します。バッフルにより、旋回流だけでなく上下方向の循環流も発生していることが確認できます。
図3-1 検討1における垂直断面の流速分布[m/s]
図3-2 検討1における水平断面の流速分布[m/s]
図4-1 検討1における垂直断面の流速ベクトル[m/s]
図4-2 検討1における水平断面の流速ベクトル[m/s]
図5に、攪拌層内の粒子の様子(アニメーション)を示します。
また、攪拌翼に作用したトルクを確認したところ、おおよそ0.7~0.9 N・mの範囲で推移し、15秒以降からは安定し平均0.78 N・mの結果が得られました。
図5 検討1における攪拌層内の粒子分布

底面に粒子が溜まっているだけでなく、流れが衝突している箇所やバッフルの後背域など、一度流速が小さい領域に粒子が捉えられると、そこから抜け出せなくなり、粒子が集合してしまう結果となりました。
(補足:本モデルでは、粒子のパラメータとして凝集力は定義していません。純粋に流れによって粒子が集合した結果になります)
図6に、水槽を4個の領域(下段/上段、内側/外側)に分け、各領域に含まれる粒子数をカウントした結果を示します。(※ 体積が等しくなる様に領域を分割しています)
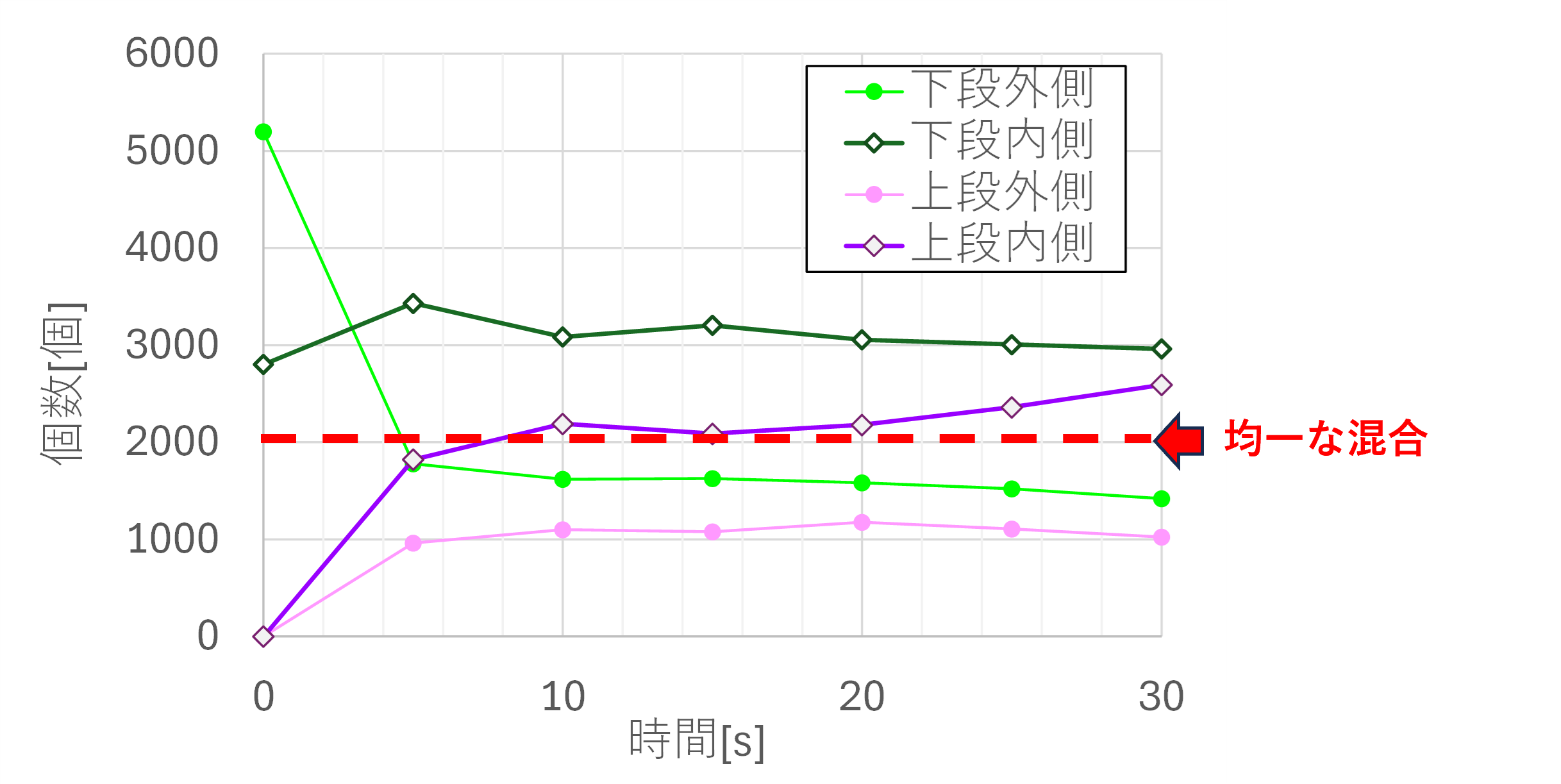
図6 各領域の粒子数(検討1)
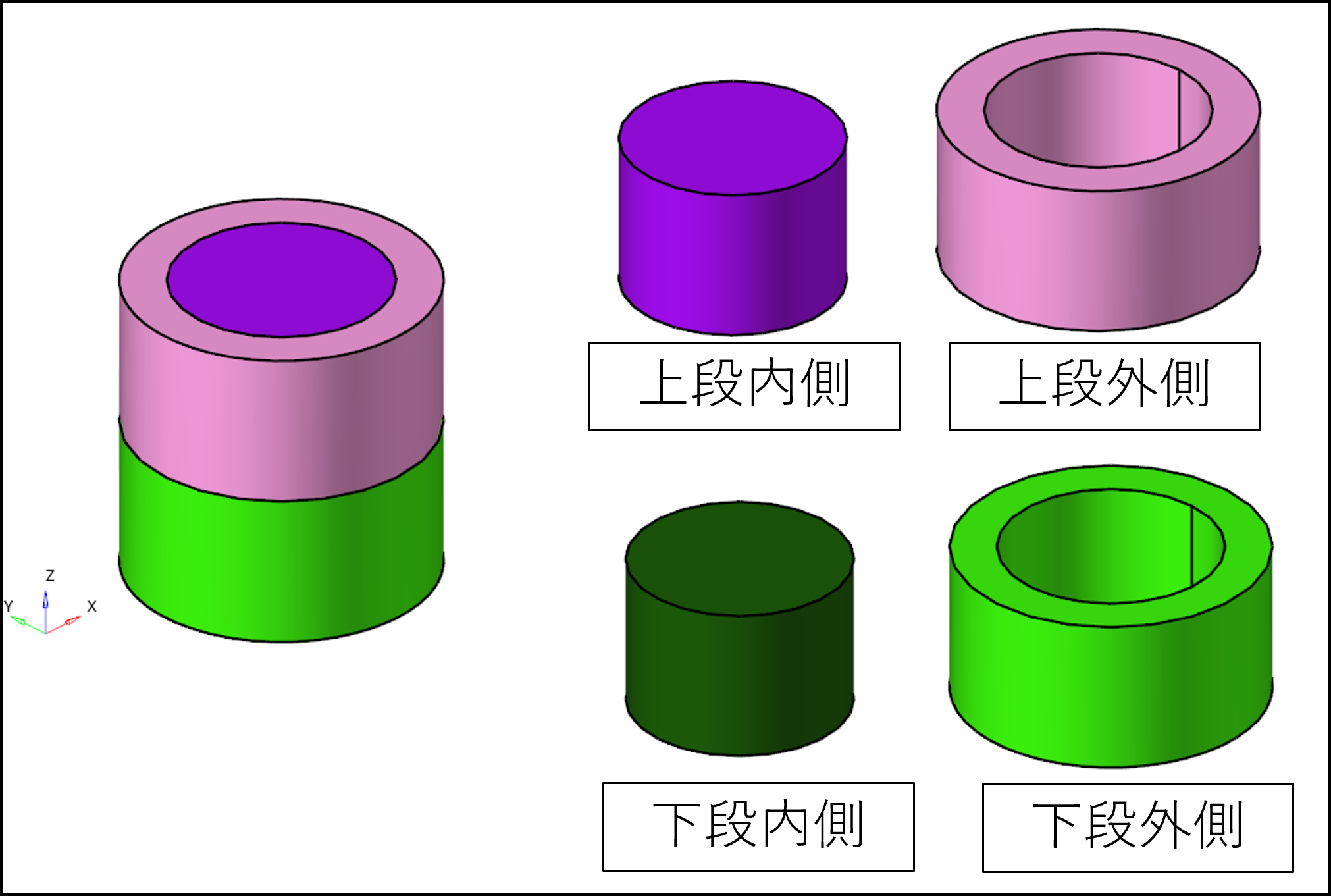
図6からも、粒子が均一に分布していないことが確認できます。図3と図4の槽内の流速分布から、バッフルによる上下方向の循環流が確認できていましたが、これだけでは固液攪拌には不十分なようです。
10 RPMではトルクの上限にまだ余裕があるため、次のステップとして角速度を20と30RPMに変更し、粒子の混合状況を調査します。
検討2:角速度の検討
シミュレーションでは簡単に条件変更した計算が行えるため、検討1のモデルから角速度だけ変更した計算を2ケース実施してみます(20RPMと30RPM)。表4に計算条件を示します。
表4 検討1~2の計算条件
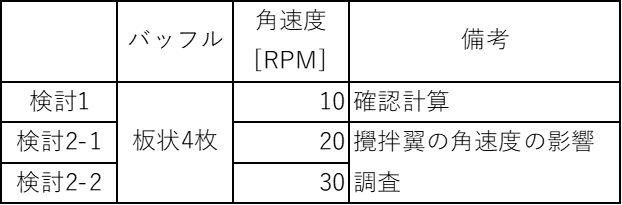
図7に、検討2の攪拌層内の粒子の様子(アニメーション)を示します。
図7-1 検討2-1における攪拌層内の粒子分布
図7-2 検討2-2における攪拌層内の粒子分布
角速度を大きくしただけでは、粒子の集合を解消することはできませんでした。特に今回は粘度が低いこともあり、角速度が大きいと遠心力によって粒子が壁面近傍に押しやられ、かえって集合しやすくなる傾向が見られました。
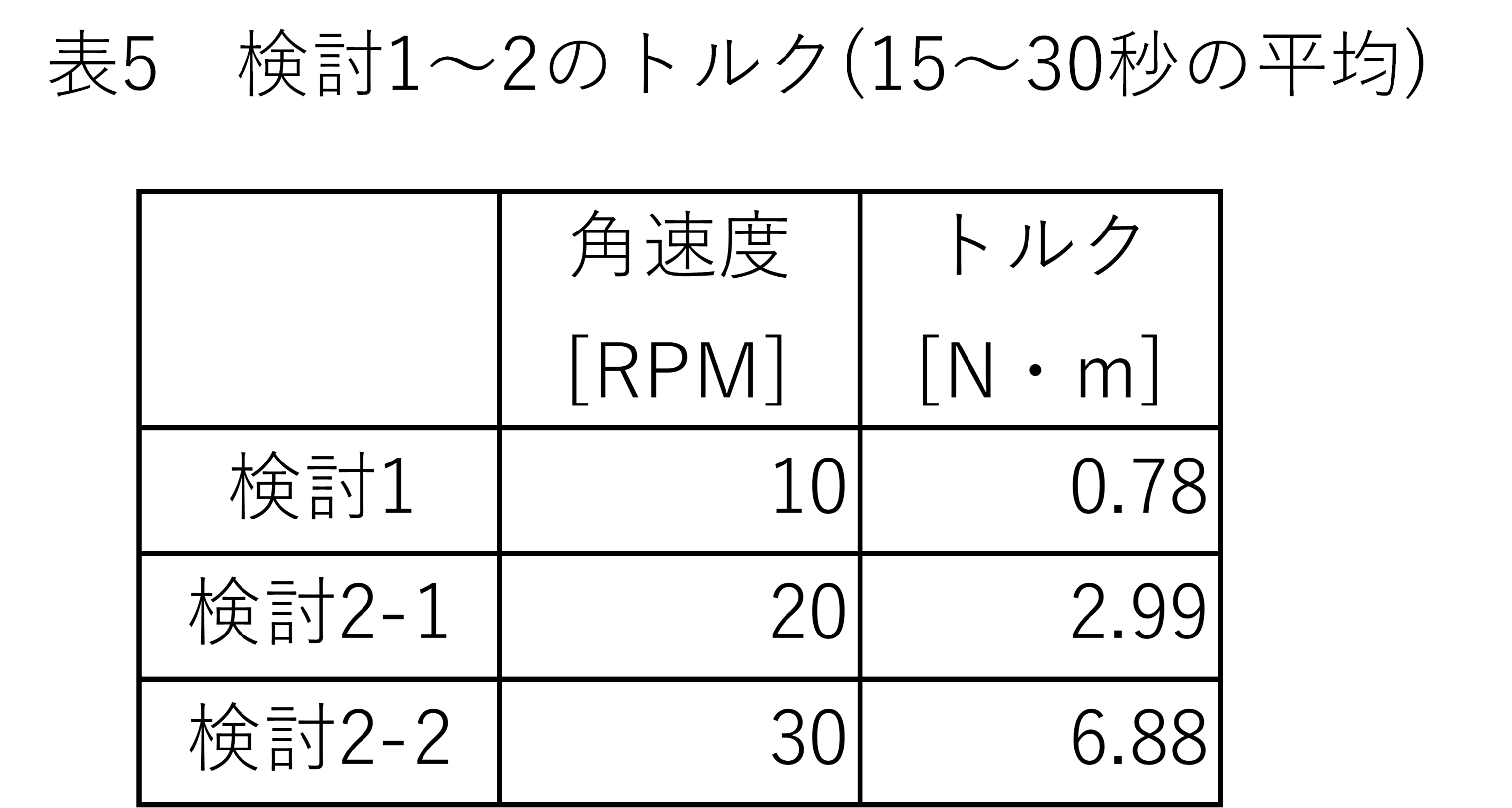
表5に攪拌翼のトルクを示します。今回設定したトルクの上限(4 N・m)を考えると20RPM程度が限界のようです。
以上により角速度の調節だけでは、粒子を均一に混ぜるのは難しいことが推測できます。次のステップでは、バッフル(邪魔板)を変更し、粒子の集合を解消できるか試してみます。
検討3:バッフル形状変更
粒子の集合を解消する別の方法として、バッフル形状の変更を検討します。シンプルな板状に切り欠きを追加してせん断速度を増加させるなど、形状修正による様々な効果が報告されています。今回は、板状のバッフルに穴を開けた形状で試してみます。穴を開けたことにより、バッフル後背域の流速が遅くなってしまう領域の解消と、流体が穴を通過する際に発生する乱れの効果により、粒子の集合が改善するかもしれません。さらに、底面にも粒子が留まっていたため、バッフルの下部をカットし、底面近傍の流速を速くしてみます。
実験では形状変更に加工費用がかかるだけでなく、一度穴を開けてしまうと元に戻すのが大変ですが、シミュレーションであれば、思いつくままに形状変更が可能です。表6に、検討3までの計算条件を示します。
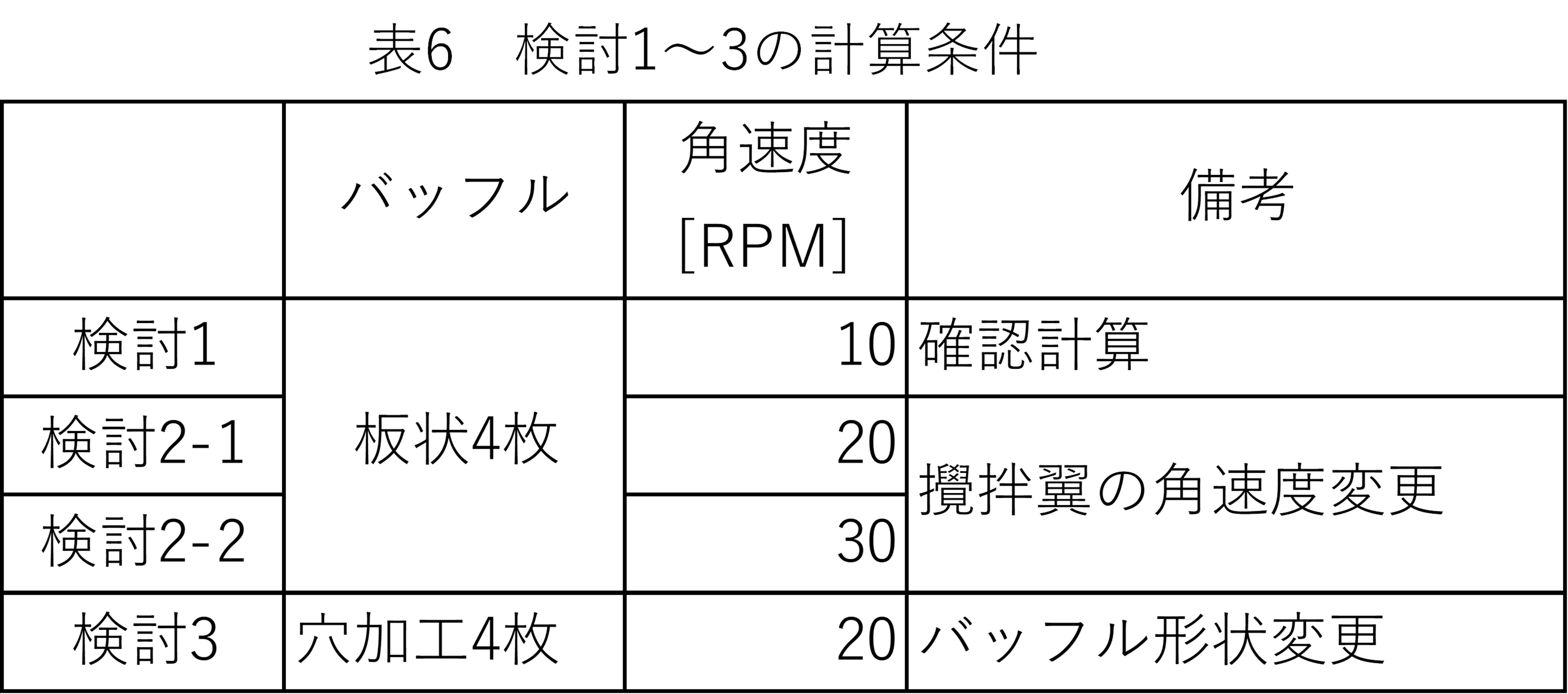
図8に検討3のモデル概要図を示します。検討1や2の流速結果からは、一定時間経過すると槽内の流れは安定し、流れの向きが頻繁に変化する様子は見られませんでした。粒子の集合解消には流れが複雑に変化した方が効果が大きいかも知れませんので、バッフルに開ける穴の高さ位置を板ごとにズラしてみます。
なお、バッフルの形状以外は、検討2-1と同じ計算条件とします。
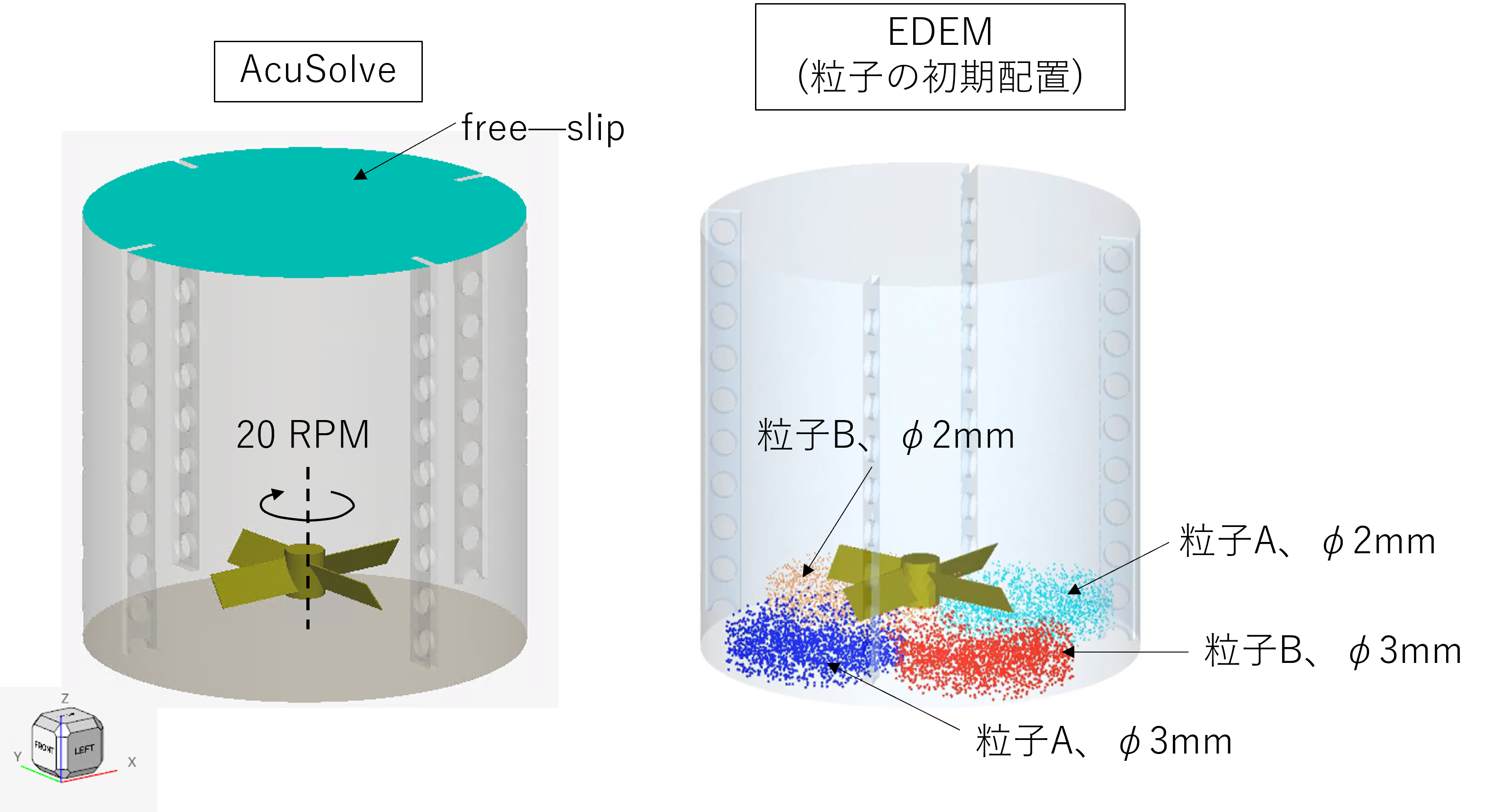
図8 検討3のモデル図
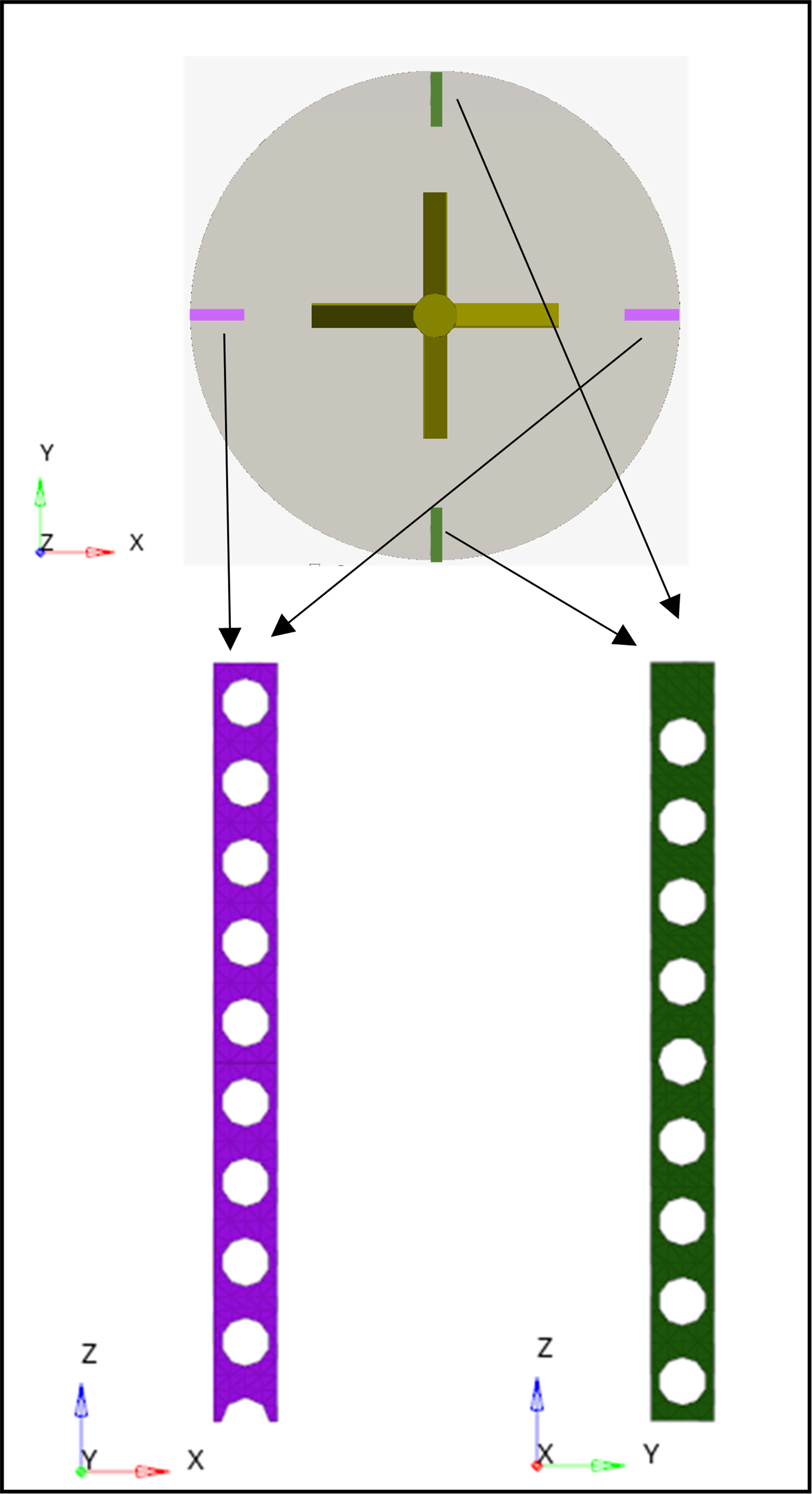
図9と図10に、各断面の流速分布と流速ベクトルを示します。
図9-1 検討3における垂直断面の流速分布[m/s]
図10-1 検討3における垂直断面の流速ベクトル[m/s]
図9-2 検討3における水平断面の流速分布[m/s]
図10-2 検討3における水平断面の流速ベクトル[m/s]
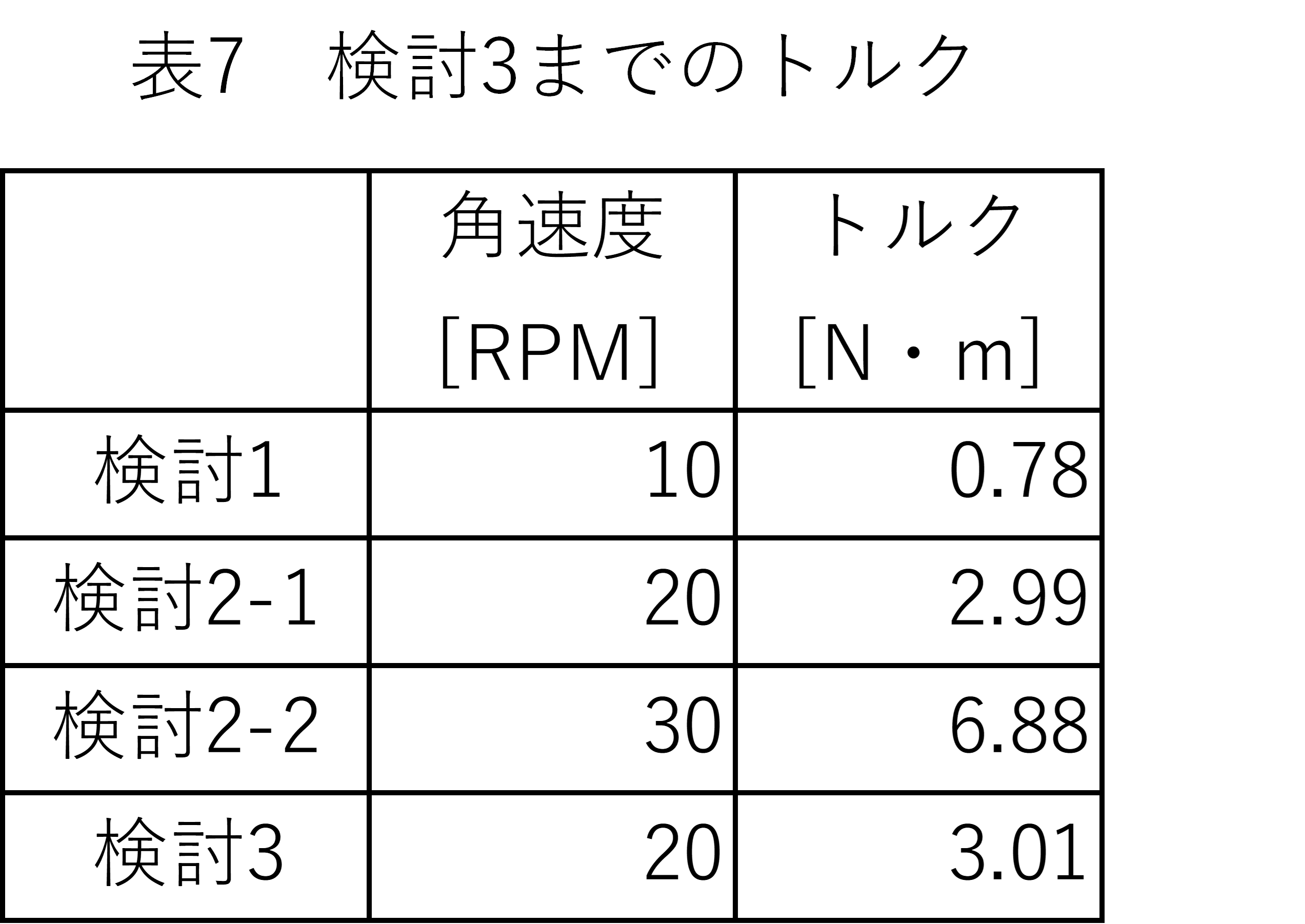
図11に、代表時刻における攪拌層内の粒子の分布を、表7に検討3までの攪拌翼に作用したトルク示します。
図11 攪拌層内の粒子分布(検討3)
翼の先端や直下にまだ粒子の集合が残っていますが、検討2にくらべ大幅に改善することができました。全体的に見てバッフルの形状変更は効果がありそうですので、次のステップではさらに形状を変更し粒子の集合を解消できるか試してみることにします。

図12 検討3の粒子の攪拌状況
検討4:パイプ状のバッフル
バッフルを攪拌槽壁面ではなく蓋に設置すると、バッフルの着脱が容易になり、攪拌対象・目的ごとに適切なバッフルに変更した攪拌が可能となります。今回は着脱式に変更し、さらに板状ではなくパイプ状のバッフル(丸棒バッフル)を複数配置して計算してみます。パイプの間隔を調節することで粒子が集合しにくくなるかもしれません。
また、検討3では攪拌翼直下に粒子が溜まっていたため、ボスの形状も一部変更してみます。
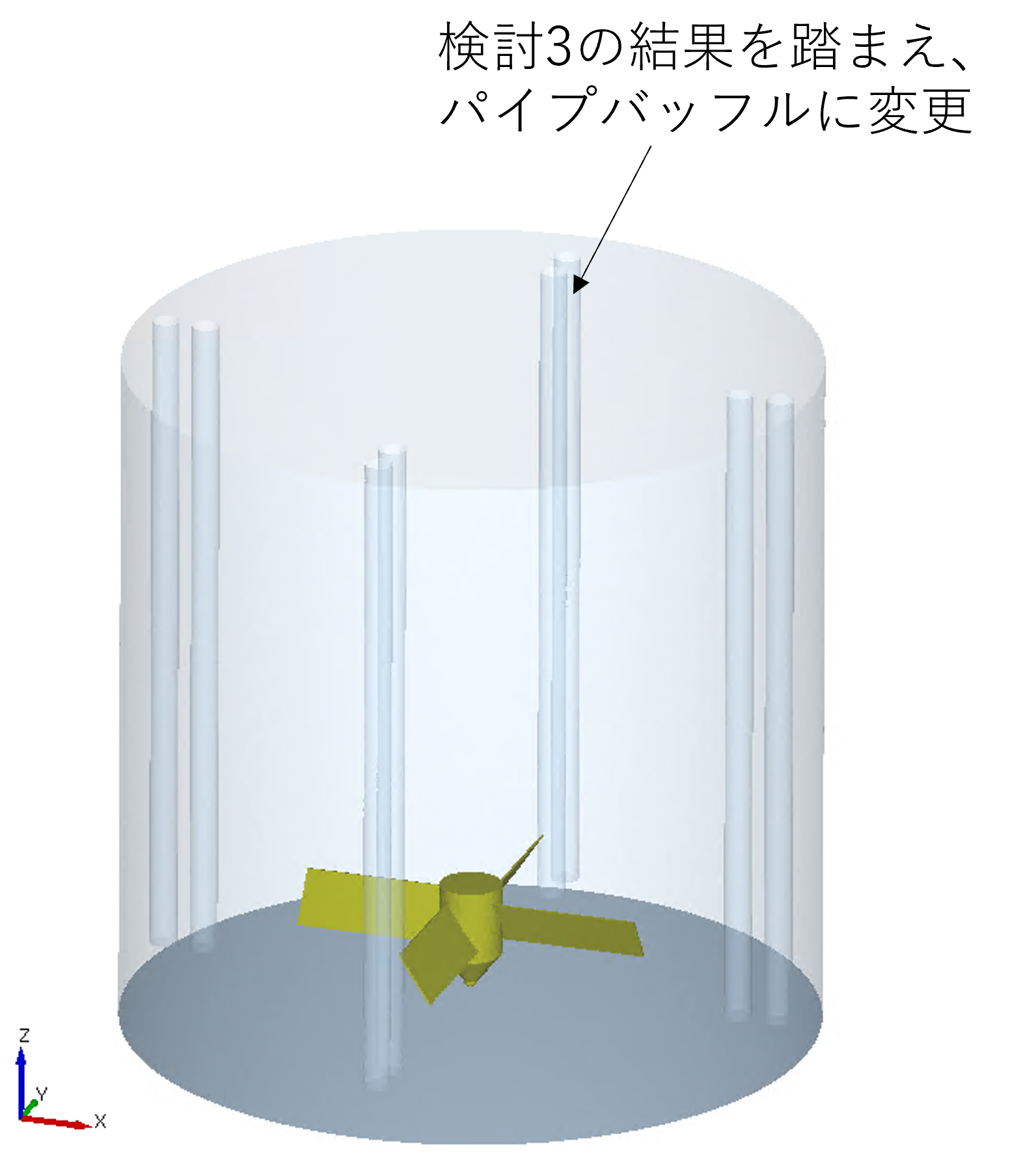
図13 検討4のモデル概要
表8 検討4までの計算条件
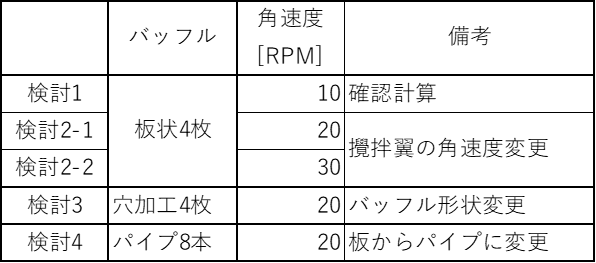
図14に検討4のモデル概要図を示します。検討3ではバッフルに開ける穴の位置(高さ方向)をズラしましたが、検討4でも、攪拌槽からの距離をズラしてみます。
なお、バッフルの形状以外は、検討2-1と同じ計算条件とします。
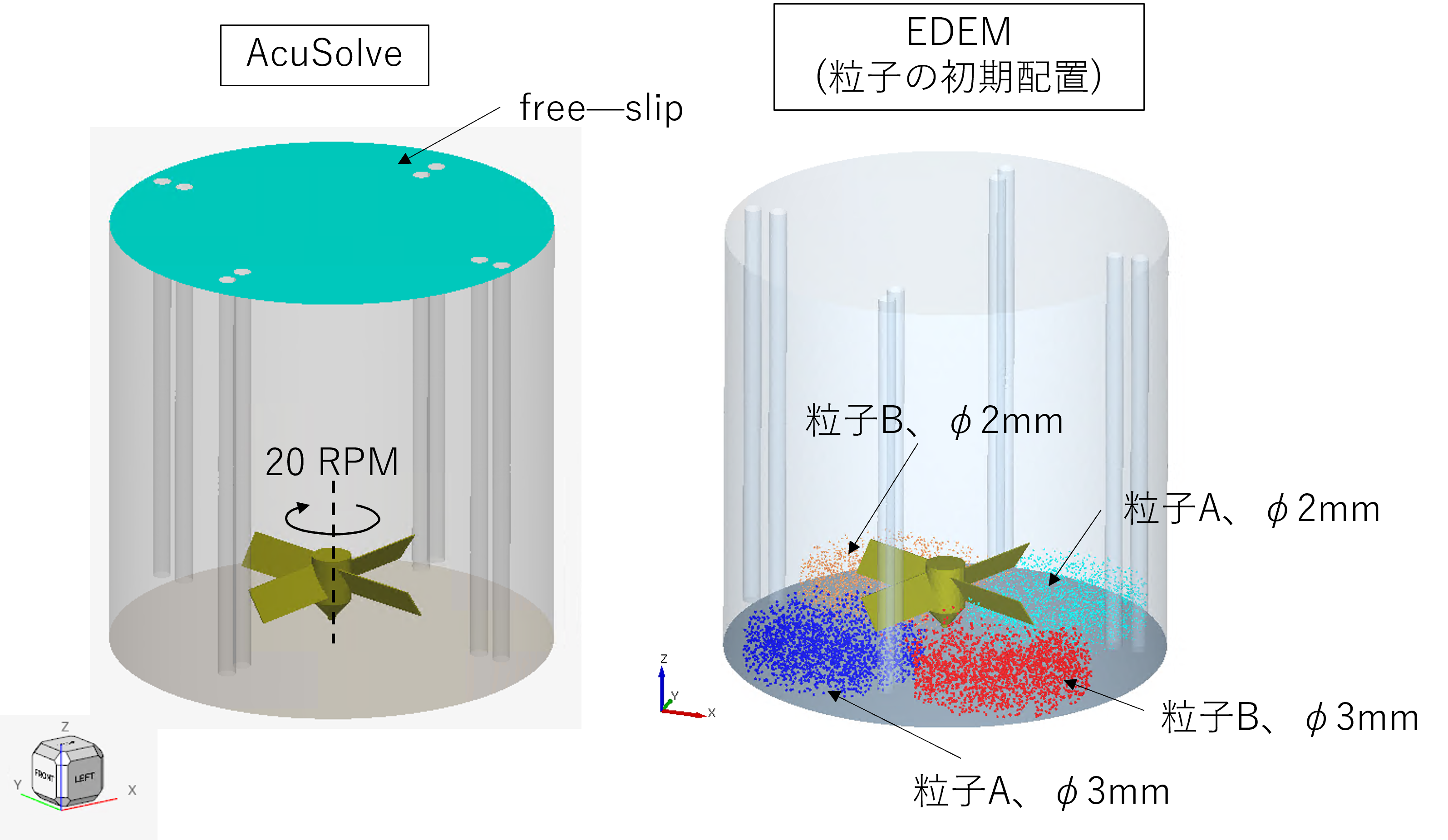
図14 検討4のモデル図
図15に、検討4における攪拌層内の粒子の分布を示します。表9に、検討4までの攪拌翼に作用したトルクを示します。
図15 攪拌層内の粒子分布(検討4)
表9 検討1~5までのトルク
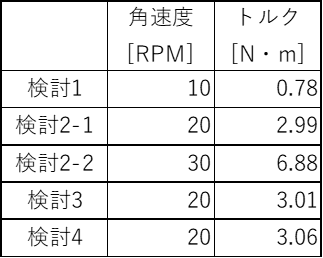
図16に、各ケースの30秒における粒子の分布状況を示します。パイプ状のバッフルにした検討4では、翼の先端や直下に粒子が残ってしまう問題も解決できています。
図16 各ケースの30秒における粒子分布
図17に、水槽を4個の領域(下段/上段、内側/外側)に分けた際の、各領域に含まれる粒子数を示します。(※ 体積が等しくなる様に領域を分割しています)
まだ改善の余地はありますが、図6に示した検討1の結果に比べ、粒子が均一に攪拌されている事が確認できます。
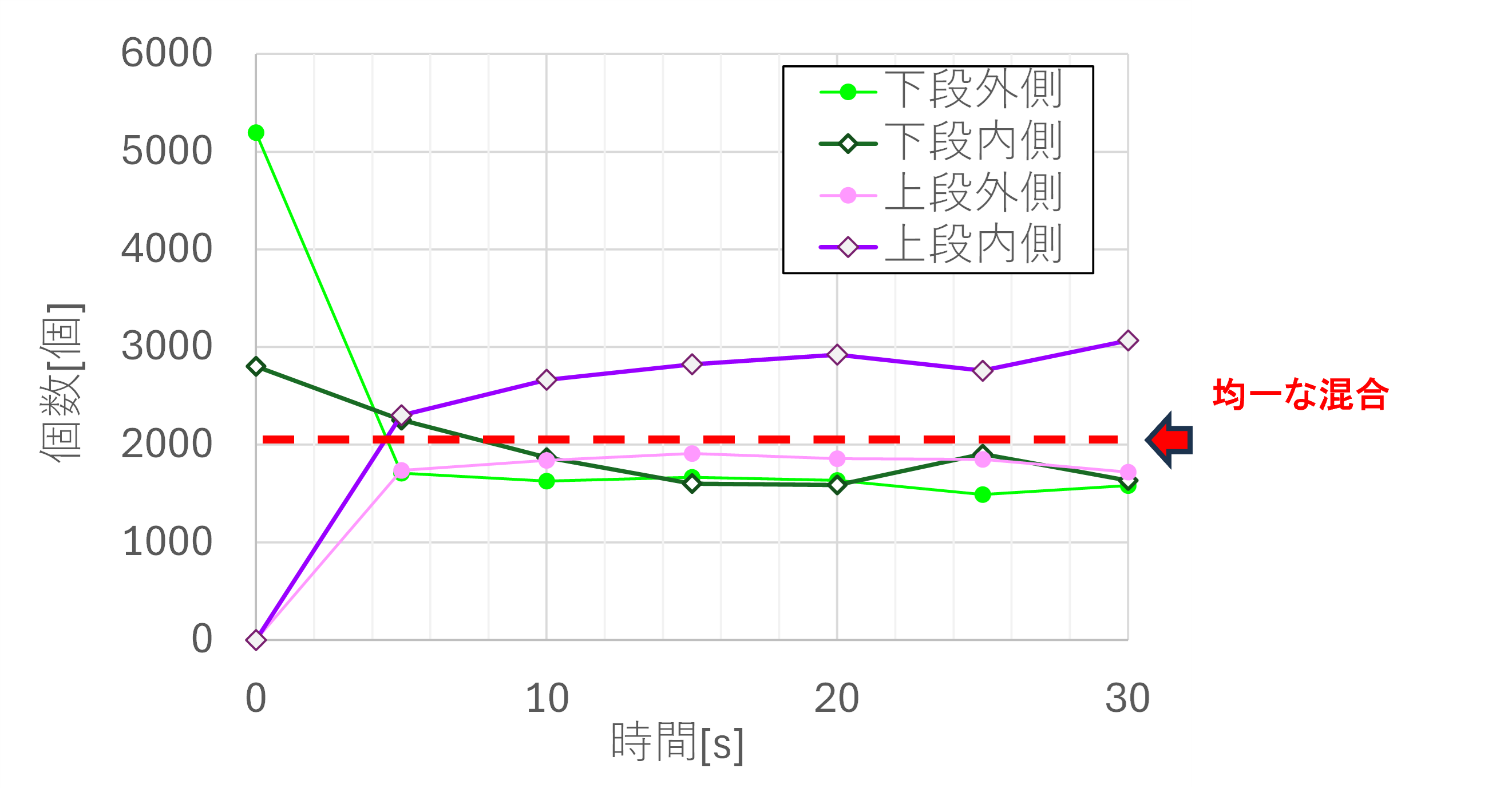
図17 各領域の粒子数(検討5)
まとめ
流体解析(CFD)ソルバーAcuSolveと個別要素法(DEM)ソルバーEDEMを連成し、攪拌層内の粒子の混合状況を調査しました。
・ シミュレーションでは、実験に比べ少ない工数で攪拌条件を変更した際の攪拌層内の粒子の様子を確認できます。
・ 実験ではコストがかかってしまうバッフル形状の変更も、シミュレーションであれば簡単に調査することができます。
・ AcuSolveは攪拌翼にかかるトルクを出力できるため、回転機器の性能と照らし合わせた条件検討が可能です。
・ EDEMは定義した領域内の粒子数をカウントできるため、攪拌状況を数値データとして確認可能です。
AcuSolveとEDEMを利用することによって、実スケールで攪拌層内の粒子挙動を計算することができるため、適切な攪拌条件の検討にご活用いただけます。