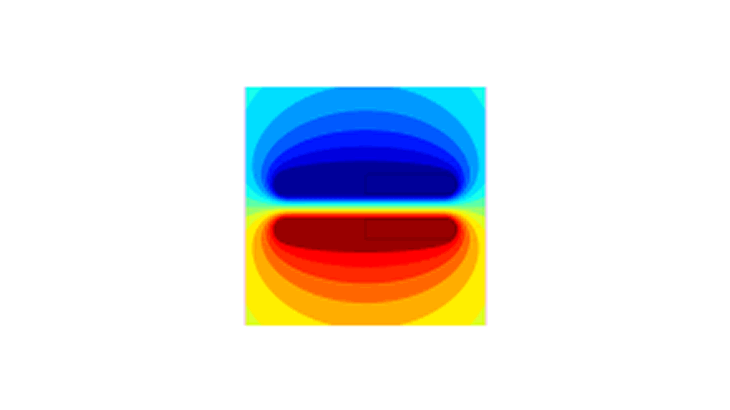
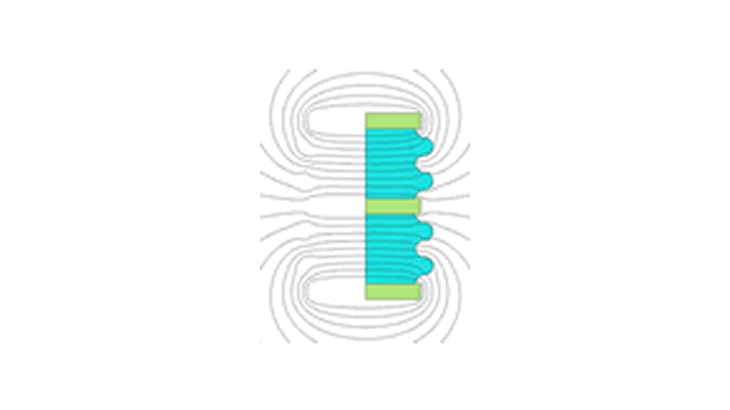
Electroは伝送線路の回路パラメータを計算することができます。境界要素法による静電界計算を利用して、効率的に伝送線路のキャパシタンスや特性インピーダンスを計算します。
1 ストリップライン モデル1
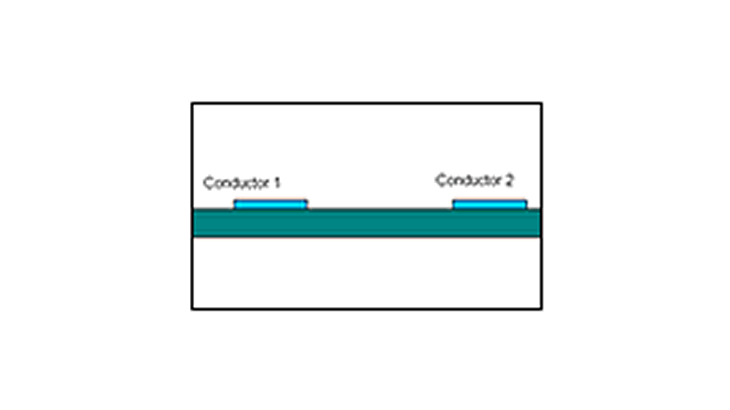
モデル1は一対のストリップラインです。解析モデル形状を図1に示しています。上面の2つのコンダクタは厚みのないサーフェスコンダクタとしています。下面はグラウンドのコンダクタです。誘電体基板の比誘電率は10とします。このモデルに対して、偶数および奇数モードのキャパシタンス、特性インピーダンス、有効比誘電率などを計算します。
2 モデル形状
解析モデルはストリップラインの2D断面をモデル化しています。コンダクタはサーフェスコンダクタで表現しているので、上面のセグメントをコンダクタ部分で分割しています。
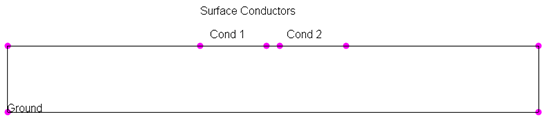
【図1 解析モデル形状】
3 解析条件の設定
(1) 誘電体の設定
誘電体基板のリージョン(青色の部分)に比誘電率10の材料を設定します。

【図2 誘電体の設定】
(2) コンダクタの設定
サーフェスコンダクタとして、上面にコンダクタ番号1と2のコンダクタ、下面にグラウンドのコンダクタを設定します。

【図3 コンダクタの設定】
(3)境界要素
ソルバーはデフォルトの境界要素法を使用します。セルフアダプティブ法を使用するので、自動的にメッシュを細分割して解析します。図4に作成された境界要素分布を示しています。境界要素数は44です。

【図4 境界要素(1D要素)】
4 計算結果
回路パラメータ解析では、ひとつのコンダクタを1 [V]に設定し、その他のコンダクタを0 [V]にして計算します。これをすべてのコンダクタについて計算することにより、キャパシタンスマトリックスなどを計算します。
個々のマトリックス成分を出力することは可能ですが、ここでは外部ファイルに一括して出力します。キャパシタンス、自由空間キャパシタンス、自由空間インダクタンスおよび特性インピーダンスマトリックスが出力されます。
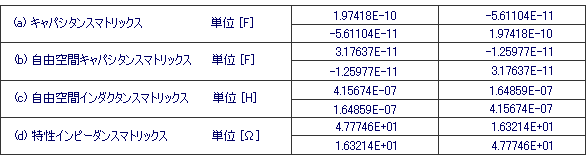
【表1 出力マトリックス】
これから偶数および奇数モードのキャパシタンスなどを表2のように計算することができます。偶数モードはコンダクタ1と2に同じ1 [V]の電位、奇数モードはコンダクタ2に-1 [V]の電位を与えたときの結果です。

【表2 回路パラメータ】