最適化支援ツールHyperStudyを利用したJMAGの形状最適化事例を紹介します。
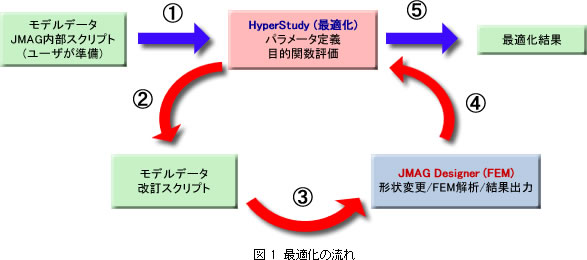
最適化の流れは図 1の通りです。
- JMAGのモデルデータと寸法変更を制御するスクリプトファイルを用意します。スクリプトファイル内の寸法情報を変数とします。
- HyperStudyにより変数部分を実数化したスクリプトファイルを出力します。
- プリ・ポストプロセッサおよびソルバーをスクリプトでコントロールし、解析結果を出力します。
- HyperStudyで解析結果を読み込み、目的関数の評価を行います。
- 最適化結果を出力します。
2~5 は収束するまで繰り返されます。
概要
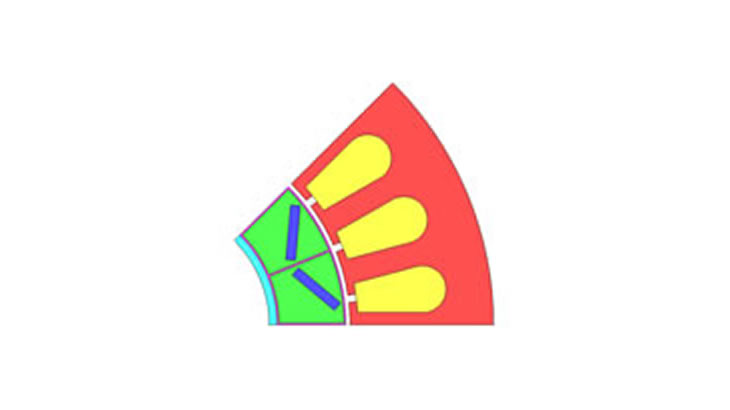
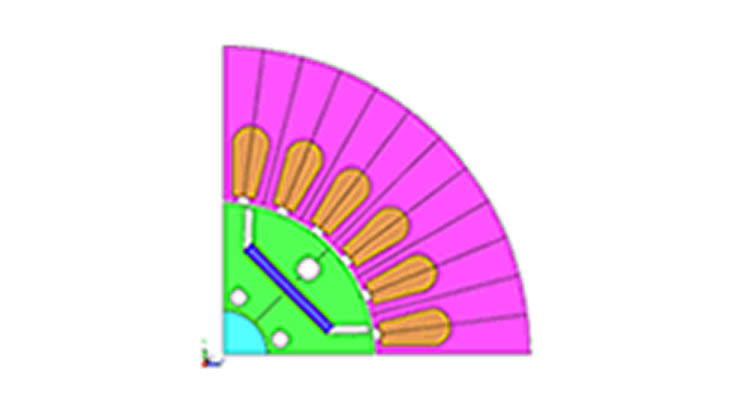
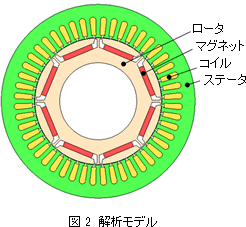
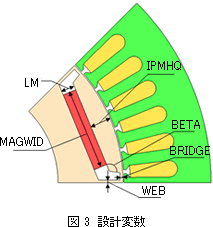
本事例ではモータの形状最適化を紹介します。 図 2に示す8極48スロットIPMモータの定常運転時の平均トルクを評価します。対称性を考慮して2次元、1/8対称(反周期境界)でモデル化します。図 3に示す寸法を設計変数とし、最適解を求めました。
解析結果
ラテン超方格計画に基づく設計変数の組み合わせを100ケース生成し、各組み合わせ条件においてFEM解析を行います。
図 4に平均トルクに対する各設計変数の影響度を示します。磁石の幅MAGWIDが平均トルクに大きく寄与していることが分かります。
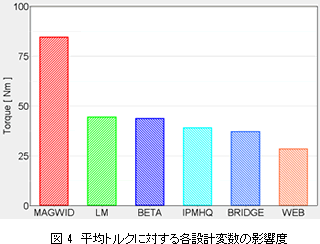
目的関数を平均トルク最大化、磁石面積最小化として最適化を行います。
表 1に示す3ケースの手法で最適化を実施し、結果を比較します。
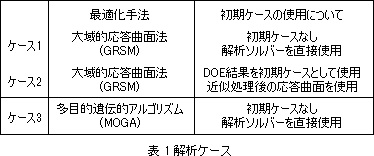
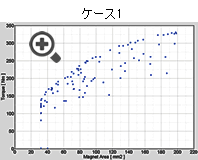
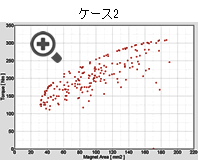
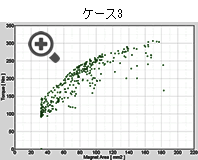
図5に各ケースにおける解分布を示します。
ケース1とケース3を比較すると、解分布に同一の傾向がありますが、多目的遺伝的アルゴリズムを利用したケース3ではパレート解を形成するまでに多くの実行数を必要とします。ケース2はケース1よりも実行数は多いですが、応答曲面を利用するためケース1よりも高速に最適解を得ることが可能です。
図 6に3ケースのパレート解の比較を示します。
3ケースとも同一の結果を得ることができました。
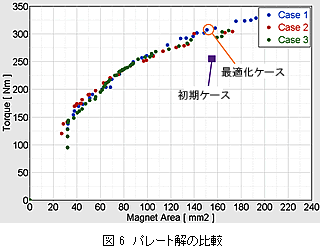
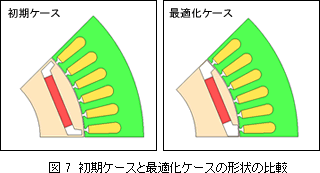
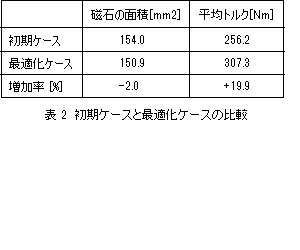
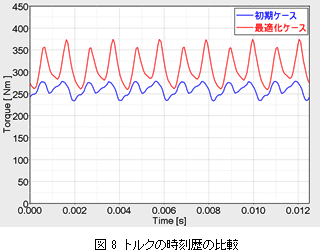
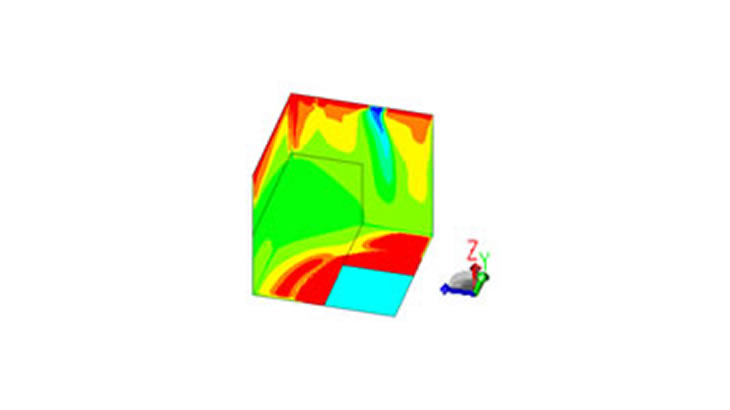
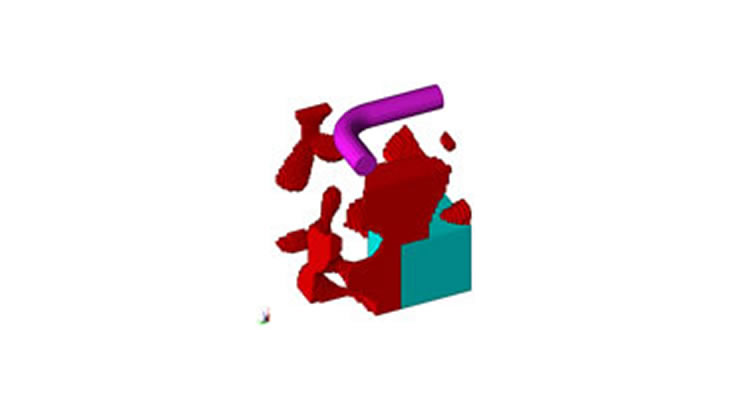
図 7に初期ケースと最適化ケースの一つとの形状の比較、表 2及び図 8にトルクの比較を示します。
磁石の使用量を維持しつつ、平均トルクを向上させることができました。