解析事例　OpenFOAM Open source Field Operation And Manipulation

電磁場－流体連成解析　ハルトマン流れの検証解析

電磁場－流体連成解析　ハルトマン流れの検証解析

はじめに


溶融金属やプラズマは電流が流れる導電性の流体です。電磁場中のこれらの流体を解析する場合、電磁力の影響を受けて流れが変化するため、電磁場解析と流体解析を組み合わせて解く必要があります。この学問分野は、電磁場の影響を考慮した流体力学であり、電磁流体力学（magneto-hydro-dynamics:MHD）と呼ばれます。

電磁流体力学の理論解が得られている問題として、ハルトマン流れがあります。

ここでは、弊社が開発したOpenFOAMのソルバーを使用し、理論解と比較、検証した事例を紹介します。

 

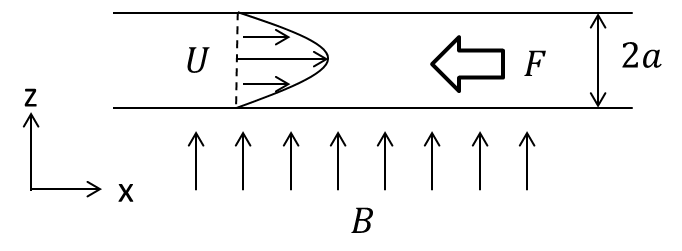
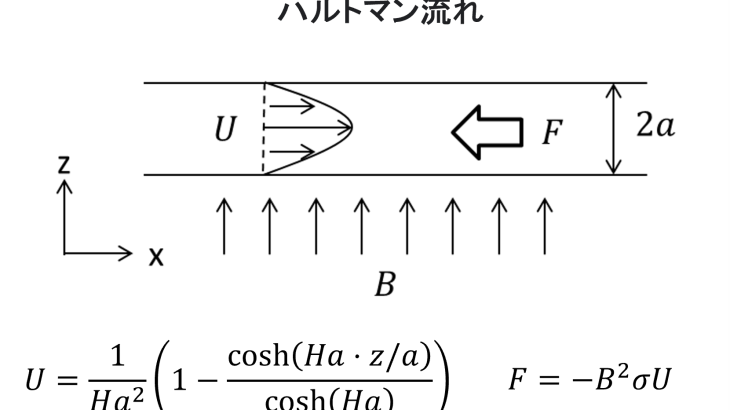
図1. ハルトマン流れ

ハルトマン流れの理論解

平行平板を流れる溶融金属に、垂直な磁場をかけた場合を考えます。並行平板はX,Y方向に無限に続いているとし、磁場はZ方向に一様一定で端の影響を無視できるとします。以下の理由から、ローレンツ力は溶融金属の流れを妨げる方向に働きます。

  1. 溶融金属（マイナス電荷の自由電子）が+X方向に一定速度で移動すると(Ux)、定常電流は-X方向に発生する(Ix)
  2. +Z方向の定常磁場中において、フレミングの左手の法則から自由電子は+Y方向に力(Fy)が働き、移動する。
  3. 溶融金属（マイナス電荷の自由電子）が+Y方向に移動することから(Uy) 、定常電流は-Y方向に発生する(Iy)。
  4. -Y方向定常電流はZ方向磁場により、フレミングの左手の法則から-X方向の力を受ける(Fx)
  5. -Y方向定常電流が受けた-X方向のローレンツ力はその媒体である溶融金属に伝わる

磁場を大きくしていくと、ローレンツ力が大きくなり、流れが抑えられる形に流速分布が変化します。

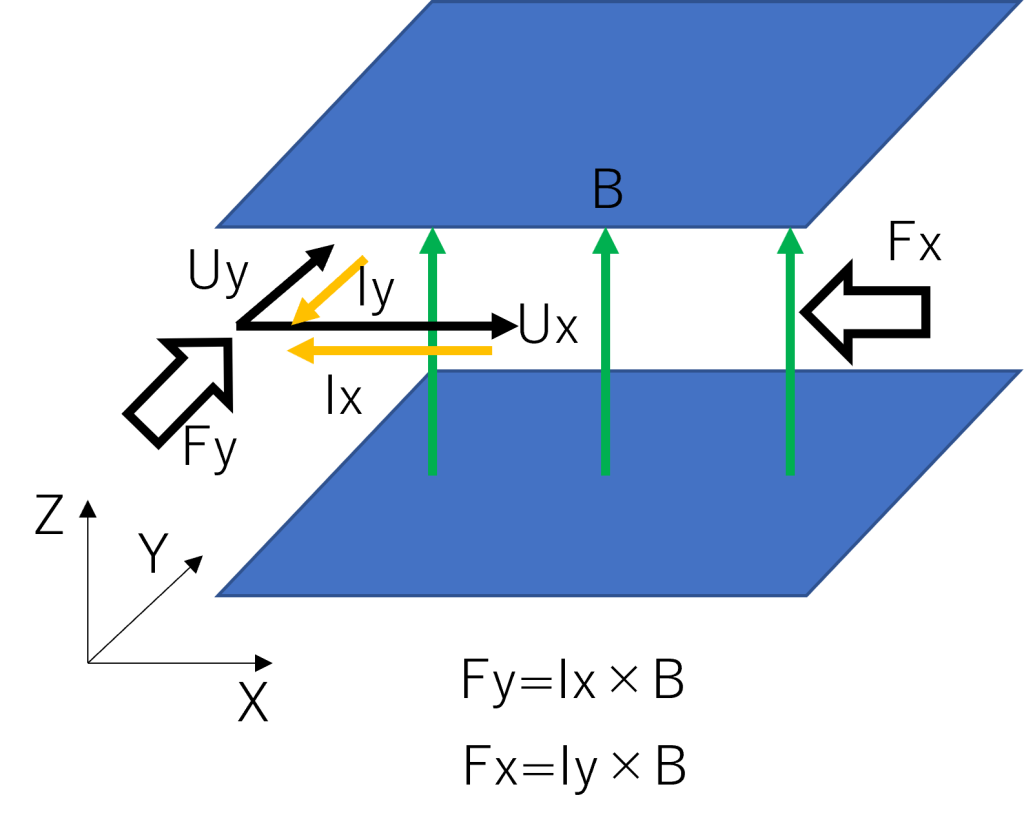
図2. ハルトマン流れの原理

流速分布はハルトマン数と呼ばれる無次元数（1）式に依存します。

このハルトマン数を使った流速分布の理論解は（2）式となります。図3に各ハルトマン数における流速分布を示します。

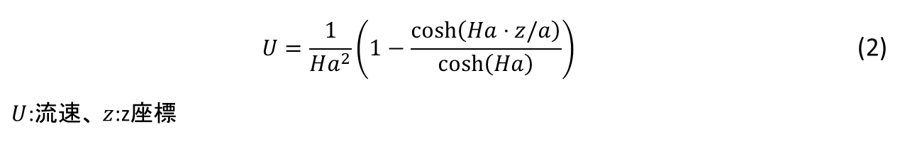
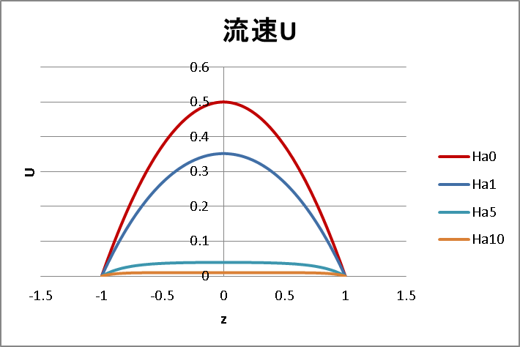
図3. 流速分布の理論解

 

また、ローレンツ力の理論解は（3）式となります。図4に各ハルトマン数におけるローレンツ力を示します。

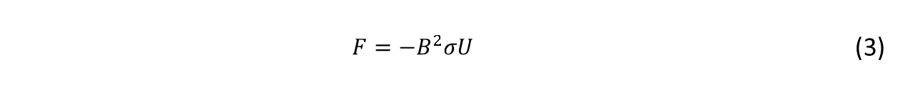
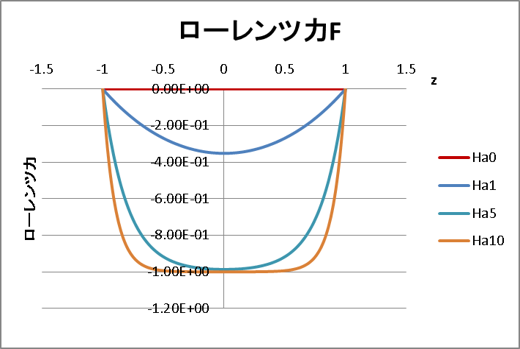
図4. ローレンツ力の理論解

解析条件

図 5に検証解析のモデルを示します。

  • 解析ソフトはOpenFOAMを使用（ローレンツ力を外力として追加するカスタマイズを実施）
  • 2次元モデル
  • メッシュは壁近傍に境界層メッシュを設定
  • ハルトマン数は4ケース実施（ Ha=0,1,5,10 ）
  • 電磁界解析は行わず、図4の理論解で求められているハルトマン数に応じたローレンツ力を、流体に働く外力として-X方向に付与

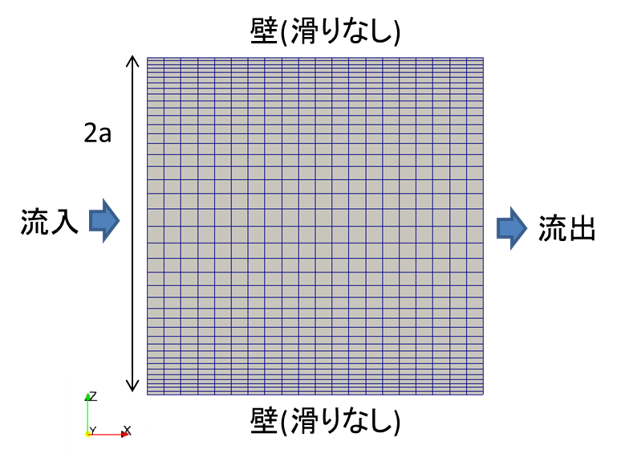
図5. 検証解析モデル

解析結果

流速分布を理論解と比較する箇所を図6に示します。ライン上のX成分速度を出力して比較しました。

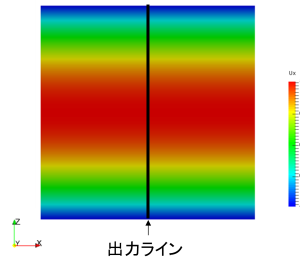
図6. 流速分布の出力個所

 

図7～10に流速分布を理論解と解析結果で比較した結果を示します。青の実線が理論解（theory）、赤の点線が計算結果（calc）を示します。理論解と良く合っている結果が得られました。

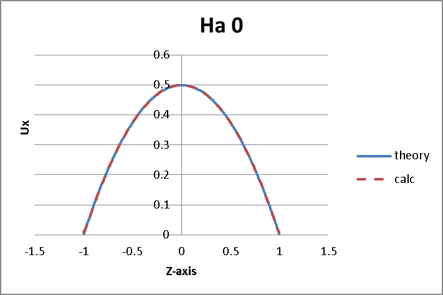
図7. Ha=0の流速分布結果

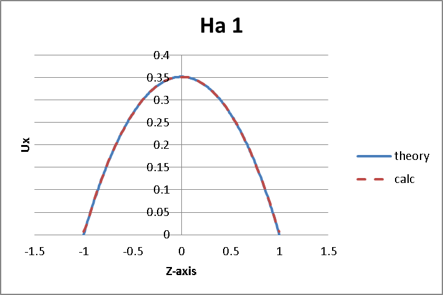
図8. Ha=1の流速分布結果

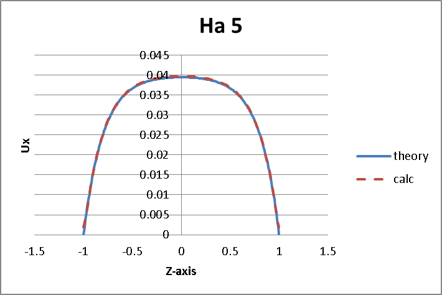
図9. Ha=5の流速分布結果

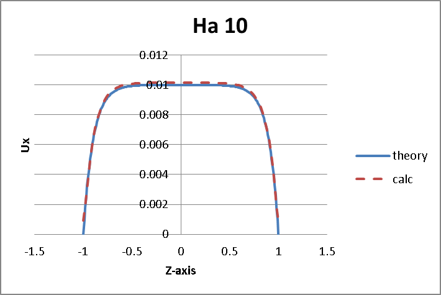
図10. Ha=10の流速分布結果

ハルトマン数が0の結果は磁場がないため、平面ポアズイユ流れに相当します。このため、図11に示す、壁面では流速ゼロで、壁面に近いほど流速の変化率が急激に大きくなる速度分布を示します。

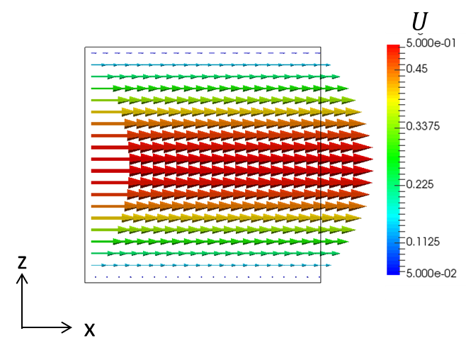
図11. Ha＝0における流速ベクトル

磁場を大きくするに従って流速が速いところほど抑えられる形となり、ハルトマン数が10の結果では、中心部分の流速が小さく平らな流速分布を示します。

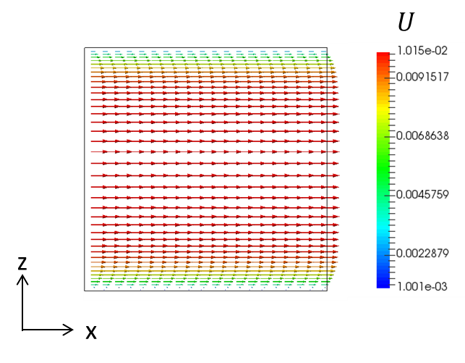
図12. Ha＝10における流速ベクトル

 

まとめ

ローレンツ力を外力として追加するカスタマイズを実施したOpenFOAMにより、流速分布の理論解を精度良く再現できることを確認しました。ハルトマン数が大きくなるにつれてローレンツ力によって流れが強く抑えられることで、平面ポアズイユ流れよりも中心部分の流速が抑えられる特徴的な流速分布を再現します。

本事例では、ローレンツ力の理論解を入力値として使用しましたが、電磁場解析ソフトで得られたローレンツ力を入力値として解析することも可能です。ローレンツ力の分布が複雑になる電磁撹拌や電磁ポンプの場合も、電磁場解析ソフトによってローレンツ力を求め、開発したOpenFOAMのソルバーに受け渡すことで流れ場の解析が行えます。

精度検証カテゴリの最新記事