やさしく見直すCAE技術 第3回「ひずみ」
身近にあっても普段あまり気づかないものに目を向け、そのものの挙動、機能、現象、原理などをわかりやすく解説するシリーズです。
今回は、物体に生じる「ひずみ」について、「応力」との関係性を交えて記述します。

第3回「ひずみ」
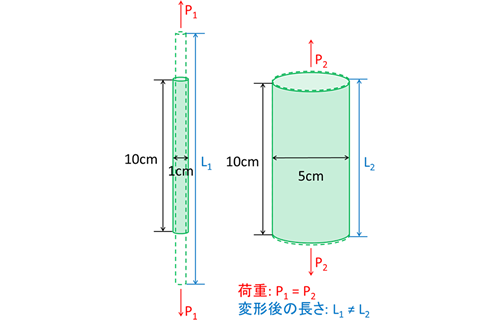
物体に「荷重」が作用すると「変形」が生じます。この荷重と変形の関係を明らかにすれば、荷重に対する変形量が推定できます。しかし、荷重に対する変形量は物体の形状によって異なります。たとえば、図1のように長さ10cm・直径1cmの棒と、同じ材料で直径が5cmの棒に同じ引張荷重を与えた場合、細い棒は太い棒よりも伸びやすい(=変形量が大きい)というのは直感的にわかります。細い棒の荷重の加わる面積は太い棒の1/25なので、細い棒に発生する応力は太い棒の25倍になります。
![]()
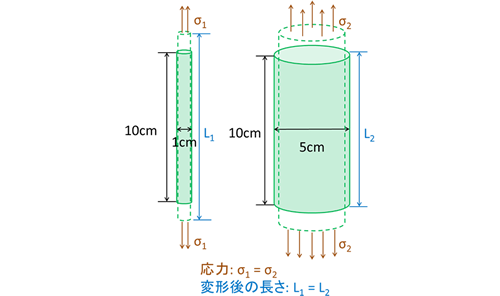
では、先述の2つの棒に同じ引張応力を与えたらどうなるでしょう(図2)?この場合、変形量は同じになります。
![]()
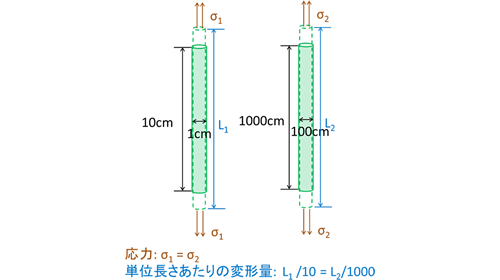
今度は、長さと直径が異なる2本の棒を考えてみます。図3のように、長さ10cm・直径1cmの棒と、長さ1000cm・直径100cmの棒に同じ引張応力を与えた場合、トータルの変形量は2本の棒で異なりますが、単位長さあたりの変形量は同じになります。この単位長さ当たりの変形量が「ひずみ(strain)」です。
![]()
荷重-変形の関係は、部材の寸法が違うとそれぞれ異なりますが、応力-ひずみの関係は、同じ材料であれば部材の寸法に関係なく同じになります。このように、応力-ひずみの関係は、材料の機械的性質を決定する重要な要素です。
材料の機械的試験で得られる応力とひずみの関係は、縦軸を「公称応力」、横軸を「公称ひずみ」とした応力-ひずみ曲線で表されます。このときの公称応力σnと公称ひずみεnは、それぞれ式(1)と式(2)になります。一方、大変形の場合は、試験片の形状変化を考慮した「真応力」と「真ひずみ」が用いられます。真応力σ’と真ひずみεlは、それぞれ式(3)と式(4)で表されます。

真ひずみεlと公称ひずみεnの間には式(4)の関係が成り立ちます。ひずみが大きいほど両者の差は大きくなり、同時に真ひずみεlは公称ひずみεnより小さくなります。たとえば公称ひずみεnが0.3の場合、真ひずみεlは0.262です。
ひずみは材料の特性に関する重要なパラメータです。土やコンクリート材料が破断する際のひずみは0.01以下です。上の例のような大きなひずみでは、鉄や樹脂など多くの材料が破断に至ります。
ストレスを受けてひずみが生じるのは人間も同じです。ストレスとひずみ量の関係に個人差があるという点も似ています。過度なひずみを貯め込まず、ストレスをうまく除荷することが構造物の健全性と長寿命化には重要ですが、これは現代社会を生き抜くうえで有用な示唆を含んでいるように思います。
関連記事/関連ページ
