やさしく見直すCAE技術 第4回「線形と非線形」
身近にあっても普段あまり気づかないものに目を向け、そのものの挙動、機能、現象、原理などをわかりやすく解説するシリーズです。今回は「線形と非線形」について触れます。

第4回「線形と非線形」
解析手法として利用される有限要素法では、微小変形で、かつ弾性領域の材料特性に限って取り扱う線形解析と、それ以外の非線形問題の両方に適用することができます。
非線形問題は、材料非線形、幾何学的非線形、境界非線形の3種類に大別できます。
材料非線形
材料非線形は、弾性範囲を超えた材料の非線形特性を扱う問題をさします。
物体に外力が作用すると物体は変形し、外力を取り除くともとの形に戻ろうとします。物質に備わるこの特性を「弾性」と呼びます。外力が十分に小さいうちは物体の変形量は外力に比例し(線形)、外力を除去すれば完全にもとの形に戻ります(弾性変形)。弾性が保たれる限界を「弾性限度」といいます。
大きな外力が働くと、物体は大きく変形し、材料は降伏して、応力とひずみの関係は非線形となります。この領域では外力が取り除かれたあとも変形が残留し、物体はもとの形に戻ることができなくなります。物質のこのような特性を「塑性」といい、このときの変形を「塑性変形」といいます。このように、材料の塑性特性を取り扱う領域が材料非線形です。
幾何学的非線形
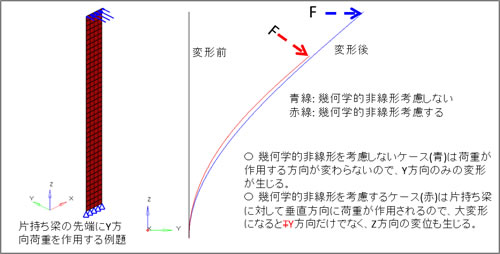
幾何学的非線形は大変形を伴う場合に生じる非線形特性です。図1に片持ち梁を用いた幾何学的非線形の例を示します。片持梁の先端に垂直に荷重が作用する場合、実際の物理現象では、変形によって荷重方向が変化しますが、線形問題では荷重方向は変わらないものとして計算します。線形問題として扱えるのは、荷重方向を固定しても結果に誤差が出ない微小変形だけで、大変形問題では変形量に応じて荷重方向を変え、実際の荷重条件をモデル化します。これを幾何学的非線形と呼んでいます。
![]()
境界非線形
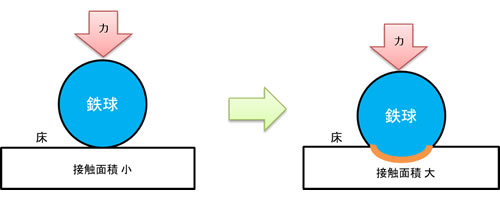
境界非線形は、境界の状態によって荷重と変形の関係に連続性が成立しなくなる特性です。主なものに物体の接触摩擦や接触圧があげられます。鉄球を床に押し付ける例を考えましょう。床のひずみが微小なときは、床にかかる荷重と変位の関係は線形です。しかしひずみが大きくなると鉄球が床に接触する面積が大きくなり、接触圧や摩擦の影響により荷重と変位の比例関係が失われます。このような効果を含む解析を行う場合は非線形性の考慮が必要になります。

実際の物理現象を詳細に観察するとなにがしかの非線形問題に該当しますが、すべてに非線形解析が必要という訳ではありません。非線形解析では計算時間が長くなりますし、収束計算のためのパラメータ調整や解析条件の設定に技術が必要とされ、難易度が高くなります。線形解析は計算コストが小さいため、得たい結果を明確にし、解析条件を限定するなどの妥当なモデル化を行えば、実用的な手段として有効に活用することができます。
計算機性能が向上し、100万節点を超える大規模な非線形解析が可能な今日となり、非線形解析がものづくりに貢献できる幅が広がりました。ですが、設計現場では、製品の品質を保証できるという意味で線形範囲の特性が設計に利用されており、計算にも時間がかからないことから線形解析が重宝されています。この要求は今後もなくならないでしょう。わたしたち解析技術者には、目的に応じた適切な解法の選択が求められます。
関連記事/関連ページ
