樹脂流動解析で用いる運動方程式

一般的な非圧縮性流れ流体解析では、運動方程式として、式(1)に示すナビエ・ストークス方程式を利用しています。
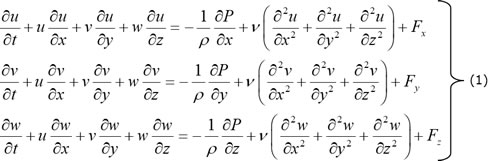
X方向の運動方程式を例に、各項の意味合いを下に示します。
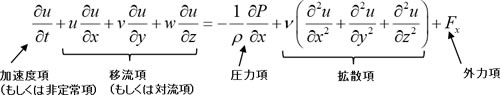
加速度項: 流速の時間変化を表わします。
移流項: 慣性的な時間変化を表わします。
圧力項: 圧力の高いところから低いところに向かう流れを表わします。
拡散項: 流体の粘性を表わします。νは動粘性係数性です。
外力項: 重力などの外力を表わします。
この時、溶融樹脂の様な高粘性流体を対象として流動を考えた場合、一般にニュートン流体では粘性の効果と移流の効果の度合いを式(2)のレイノルズ数によって見積もることができます。

L: 代表長さ
U: 代表速度
ν: 動粘性係数(=μ/ρ μ:流体の粘性係数 ρ:流体の密度)
一般的な熱可塑性樹脂では、密度に対して粘度が非常に高く、また射出成形を考えた場合、面積に対して厚みが薄いので平行平板間の流れと仮定でき、代表長さも厚みの2倍と考えられます。
これらの要因からレイノズル数が十分に小さくなり、移流の効果は粘性に比べて小さいと考えられるため、移流項を省略する事ができます。
このときナビエ・ストーク式は簡略化され、式(3)のストークス方程式が得られます。
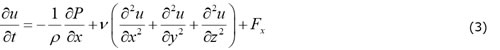
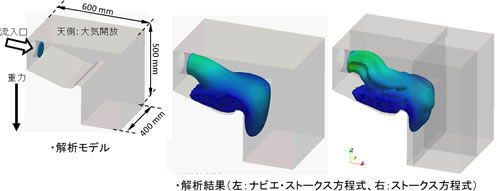
ただし、熱硬化性樹脂やウレタン樹脂など低粘性の樹脂や重力の影響による流動が生じるような成形では、ストークス方程式だと流動現象を再現が困難な場合もあります(図1)。
![]()
また、熱可塑性樹脂の射出成形での溶融樹脂の流動を考えた場合、
①充填過程では自由表面であるフローフロントが前進し、温度も時間ともに変化する非定常現象ですが、金型内の充填済み部分に視点を固定して流動現象を考えると、速度の時間変化は小さい事から定常状態と仮定した場合には非定常項が省略でき、また先に述べたように密度に対して粘度が高いため、重量などの体積力も省略すると、式(3)は式(4)のように簡略化されます。
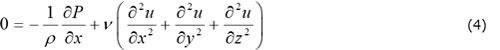
②薄板内の流れと仮定して、z方向を厚さとした場合、厚さ方向の速度wはゼロとなり、また表面で滑りのないニュートン流体の流れとすれば、板厚断面内の速度は、壁面で速度ゼロ、中心で最大となります。この時、厚さ方向の速度こう配(∂2u/∂z2)が大きく、面内の速度こう配(∂2u/∂x2,∂2u/∂y2)は無視する事ができ、式(4)は式(5)のように簡略化できます。
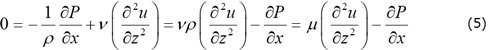
樹脂の粘性(μ)はせん断速度に依存して変化するため、せん断粘性係数となり、ηで表わします。
流動中の流体において粘性によるせん断応力τ=η ∂u/∂zとなるので、式(5)は、式(6)のように表わせます。
これは、粘性によるせん断応力と圧力こう配(∂P/∂x ) が釣り合う事を表わしています。この近似はHele-Shaw流れと呼ばれ、樹脂流動解析に古くから利用されています。

当社では、エクセルを用いて樹脂粘度の構成式やHele-Shaw流れなどの計算を行い、樹脂成形解析の理解を深める技術セミナーを実施しています。
関連記事/関連ページ
