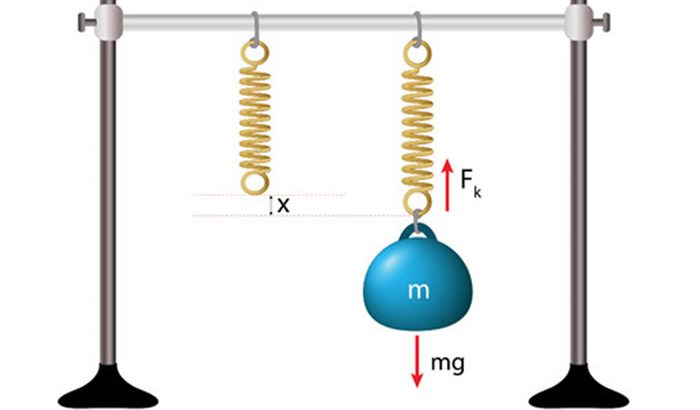
樹脂成形とレオロジー 第4回 「弾性と粘性」
今回は粘弾性体のモデル化の前段階として、フックの法則とニュートンの粘性法則について整理します。
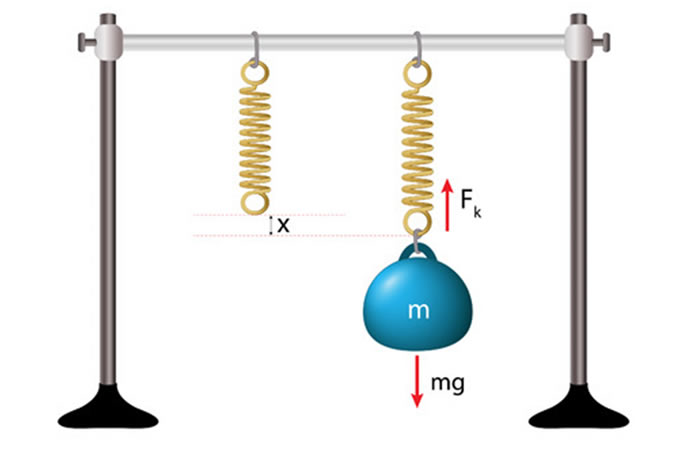

フックの法則(Hooke’s law)と線形弾性体
1676年にイギリスの物理学者ロバートフック(Robert Hooke)が「ばねの伸びと弾性限度以下の荷重は正比例する」という法則を記述しました。

弾性体は荷重を加えると変形し、除荷すると元の形に戻ります。このような弾性体は多くの場合フックの法則の形に従います。これを線形弾性体、またはフック弾性体とよびます。
![]()
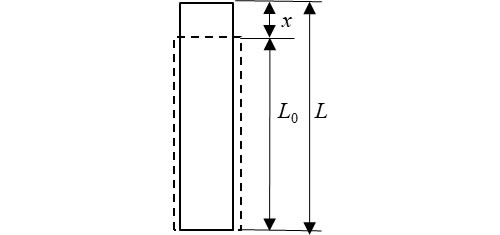
いま、図2のように棒を一方向に引っ張る状態を考えると次式が成立します。

物体の初期状態に対する総変形の比で表わすひずみを工学ひずみまたはコーシーひずみ(Cauchy strain)とよびます。元の長さをL0、伸びをxとすると次式で示されます。
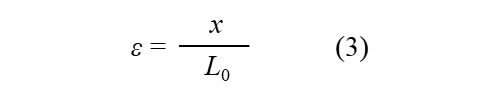
一方、ひずみ増分を積分することにより得られるひずみを対数ひずみ、自然ひずみ、真ひずみ、ヘンキーひずみ(Hencky strain)とよびます。これを次式に示します。
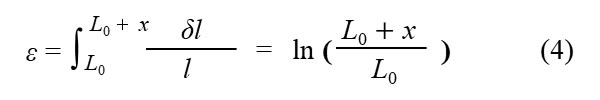
一般的には伸びた後の長さをLとして次式で表わします。
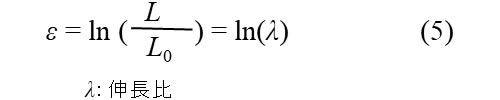
εが0.04付近までは工学ひずみと対数ひずみの差はほとんどありませんが、これ以上になると前者の誤差が大きくなり、対数ひずみを用いる必要があります。通常、プラスチック成形加工で大変形が生じる場合は対数ひずみを使って解析します。
ニュートンの粘性法則(Newton’s law of viscosity)とニュートン流体

![]()
万有引力の法則で有名なニュートンは1685年に「液体要素のすべりにくさから起こる抵抗は、他の条件が同じときに液体要素が互いに引き離される速度に比例する」という仮説を立てました。
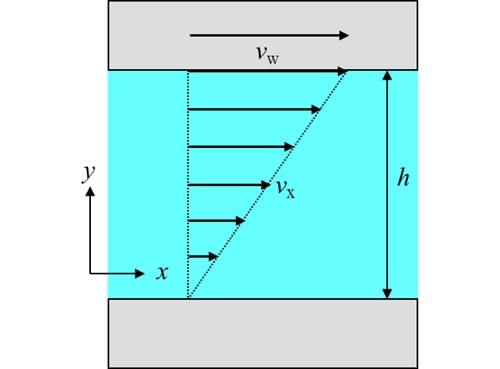
いま、図3のように平行な壁の間に非圧縮性流体が置かれ、上側の壁を一定速度で平行移動させます。流体は壁に付着する性質を持つので、下側の壁に接した箇所は動かず、上側の壁に接した箇所は壁と同じ速度で移動します。その結果、高さ方向に沿って速度分布ができます。流れが層流に保たれる場合、速度勾配は一定で、次式で示されます。

また、このような流れをクエットの流れ(Couette flow) とよびます。
![]()
このときの速度勾配はせん断速度(Shear rate)とよばれ、図3の座標系で一般的に表すと次式になります。
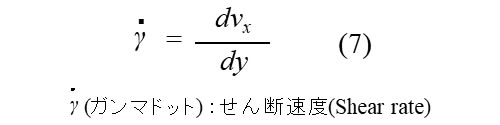
また、せん断応力τ (Shear stress)とせん断速度の関係は次式となります。

(8)式において、応力は観測時の速度勾配(せん断速度)のみに比例、すなわちηが一定のものがニュートン流体とよばれます。
なお、流体力学では通常ニュートン流体を取り扱い、粘度はμで表わす場合が多いのですが、高分子系の流れは非ニュートン性を示す場合がほとんどであり、この場合の粘度はηで表されます。
線形弾性体とニュートン流体の特性の違い
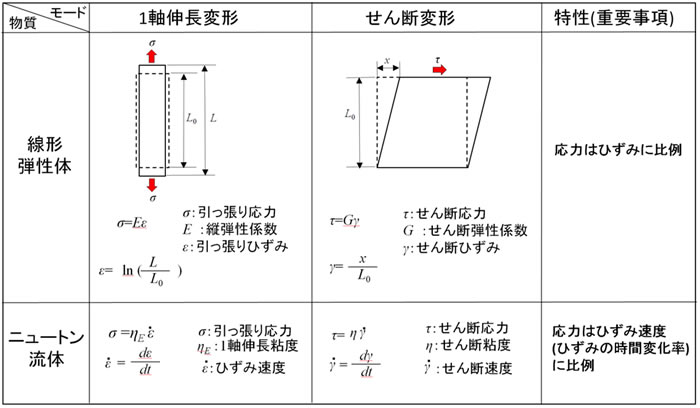
線形弾性体とニュートン流体の特性の違いをまとめます。1軸伸長変形とせん断変形のモードに分けてあります。
1軸伸長変形とは、ある軸に沿って試料が垂直に引き延ばされ、他の二軸方向は縮むモードの変形です。せん断変形とは、試料のある面に力が平行に加わり平行四辺形のようになるモードの変形です。ひずみの定義が異なりますが、線形弾性体の場合、どちらも応力はひずみに比例します。縦弾性係数Eとせん断弾性係数Gは次の関係があります。
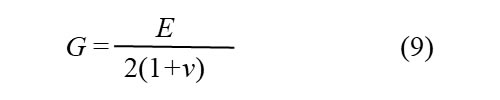
ここで、νはポアソン比(応力に直角方向に発生するひずみと応力方向に発生するひずみの比に-1を乗じた値)です。νは物質固有の値ですので、(9)式によりEとGのどちらかが分かれば、他方が求められます。
ニュートン流体の場合も変形モードにより応力を求める式の記号が変わりますが、どちらも応力はひずみ速度(せん断変形のときはせん断速度という言い方にしている)に比例します。なお、1軸伸長粘度ηEとせん断粘度ηは次の関係があります。
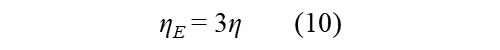
(10)式によりηEとηのどちらかが分かれば、他方が求められます。
粘弾性体のモデル化では、応力がひずみに比例する線形弾性体と応力がひずみ速度に比例するニュートン流体の特性を組み合わせて表現します。 図4のような単純な例ではE、 G、ηE、ηが材料固有の定数になり、動的粘弾性装置などを使ってこれらの値を求めていくのが一般的です。用いる試料が固体の場合は試料をチャックで掴んで1軸伸長変形モードの実験が容易ですが、液体の場合は試料を容器内に入れたせん断変形モードの実験が向いています。どちらかのモードを選んで実験すれば(9),(10)式から計算で残りの係数が求められることになります。
トリビア(豆知識)
同時代の英国人である実験派のフックと理論派のニュートンの間には各種現象の解釈をめぐって色々な確執があったようです。フックの肖像画が現存しないのはその結果だという説が残っています*。それはともかく、工学分野での力学体系はこの2人の業績に支えられています。
*中島秀人著:ロバート・フック ニュートンに消された男:朝日選書
関連記事/関連ページ