樹脂成形とレオロジー 第 5 回「 粘弾性体のモデル化 」

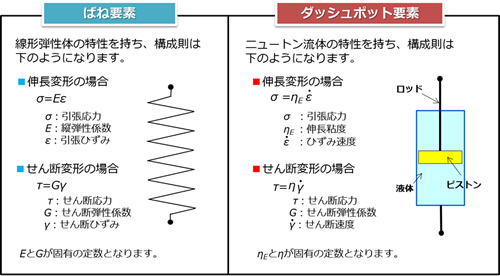
ばね要素とダッシュポット要素
プラスチックなどの高分子材料は、一定のひずみを与えておくと時間の経過とともに応力が低下する応力緩和や、一定の応力を与えておくと時間の経過とともにひずみが増加してある値に向けて飽和していくクリープとよばれる現象が起きます。これらは材料が弾性と粘性の特性を併せ持つために起こります。それぞれの単体特性を持つ要素をうまく組み合わせれば、応力緩和やクリープ現象が表現できそうです。モデルとしては弾性部をばねに粘性部をダッシュポットにしてあたかも機械要素のようにイメージするのが一般的になっています (プラスチックの中にそういうものが入っている訳ではありません)。
![]()
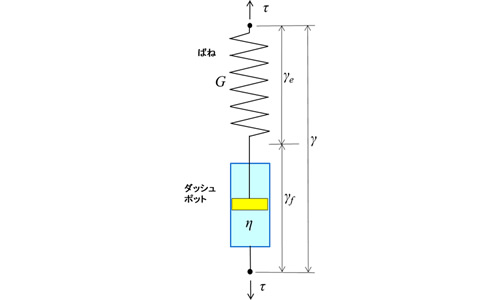
マックスウェル(Maxwell)モデル
マックスウェル (Maxwell)モデルはばねとダッシュポットを直列につないだ二要素モデルで、粘弾性体の応力緩和を表わすときの基礎になります。ここでは、ばねの弾性係数をG、ダッシュポットの粘度をη 、両端に加わる応力をτ 、ばね側のひずみをγe 、ダッシュポット側のひずみをγf 、総ひずみをγとしておきます。
![]()
■ 一般式の誘導
応力とひずみの釣り合いを表す支配方程式は次の形になります。
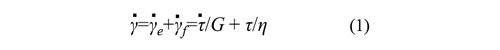
式中のドットは時間変化率です。
(1)式を書きかえると次式が得られます。
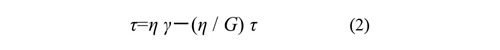
ここで次のように定義します。

λ は時間の単位を持ち、緩和時間とよばれる重要な特性値です。

■ 応力緩和現象への適用
![]()

時間t=0における応力をSとして解くと

t = λ (緩和時間)では
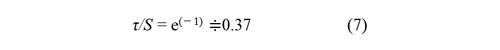
応力が初期の約37%になった時刻を緩和時間と定義できます。
■ 一定ひずみでの応力緩和
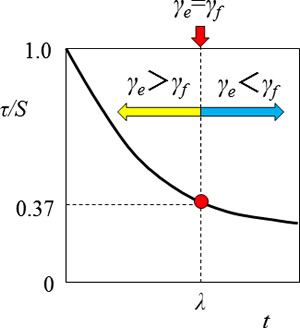
横軸に時間、縦軸に無次元応力を用いると下図になります。t <λではばね側のひずみが大きい、すなわち弾性の寄与が大きくなっています。 t =λ では両者のひずみが等しくなり、弾性と粘性の寄与が同じになります。 t >λではダッシュポット側のひずみが大きい、すなわち粘性の寄与が大きくなっています。

![]()
フォークト(Voigt)モデル
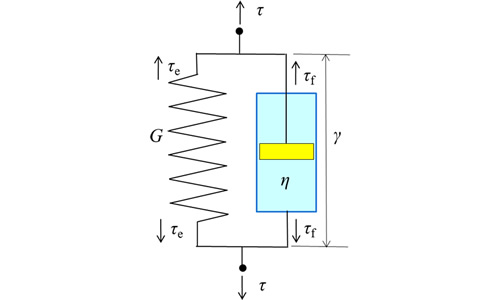
フォークト(Voigt)モデルはばねとダッシュポットを並列につないだ二要素モデルで、粘弾性体のクリープ現象を表わすときの基礎になります。ばねの弾性係数をG、ダッシュポットの粘度をη、ばね側とダッシュポット側に加わる応力をそれそれτe、τf、合計をτ、ひずみはγとします。
![]()
■ 一般式の誘導
応力とひずみの釣り合いを表す支配方程式は次の形になります。
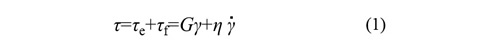
式中のドットは時間変化率です。
(1)式を書きかえると次式が得られます。
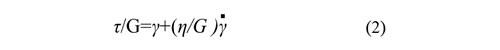
ここで次のように定義します。

tk は時間の単位を持ち、遅延時間とよばれる重要な特性値です。

■ クリープ現象への適用
一定応力をSとして(4)式を解くと
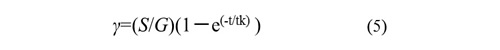
t = tk (遅延時間)では
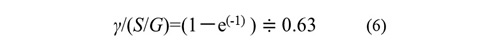
(5)式でt=∞のときにγ=(S/G)となります。このひずみは純弾性体としたときの値です。すなわち、ひずみがt=∞のとき(粘性の作用が消え、弾性のみの寄与となる)の値の63%になった時刻を遅延時間tkと定義できます。要素の定数(η と G) が同じなら遅延時間は緩和時間と同じになります。
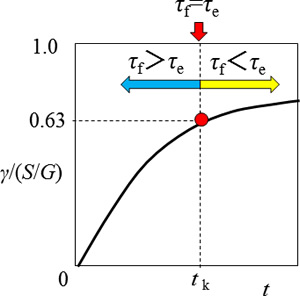
■ 一定応力でのクリープ
横軸に時間、縦軸に無次元ひずみを用いると下図になります。t <t kではダッシュポット側の受け持つ応力が大きい、すなわち粘性の寄与が大きくなっています。 t =λ では両者の応力が等しくなり、弾性と粘性の寄与が同じになります。t > t kではばね側の受け持つ応力が大きい、すなわち弾性の寄与が大きくなっています。

![]()
関連記事/関連ページ
●樹脂成形とレオロジー 第4回 「粘性と弾性」
●樹脂成形とレオロジー 第6回 「緩和弾性率の表わし方と時間・温度換算則」
