樹脂成形とレオロジー 第6回「緩和弾性率の表わし方と時間・温度換算則」

緩和弾性率とは
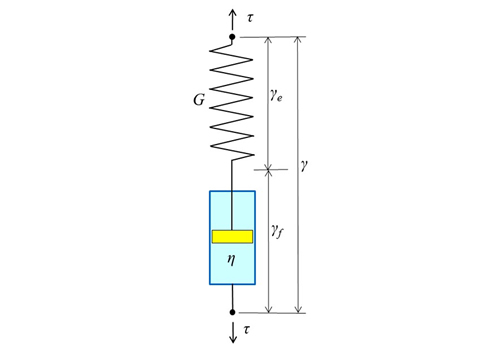
前回示したように、図1のマックスウェルモデルでひずみ一定のときは、次の応力緩和の式が得られます。
![]()
![]()
ここで、 τ(t):t秒後の応力、S:初期応力、λ:緩和時間、η:ダッシュポット粘度、G:ばね弾性率です。ひずみ量をγとして(1)式をγで除すと次式となります。
![]()
応力をひずみで除した物性値は弾性率で、右辺のS/γはマックスウェルモデルで用いたGになります。左辺は時間とともに減少する弾性率で、これを緩和弾性率とよびます。緩和弾性率はダッシュポットの作用によりGが時間とともに減少することを示しており、これをG(t)で表すと(3)式は次式となります。
![]()
すなわち、応力緩和が起きるのは材料が緩和弾性率の特性を有しているためです。
![]()
一般化マックスウェル(Generalized Maxwell)モデル
プラスチック材料は緩和弾性率の特性を有しますが、一組のばねとダッシュポットのみを用いる2要素マックスウェルモデルではフィッティング用の係数がGとλの二つしかなく、実材料の特性をうまく表せません。このため、通常は2要素マックスウェルモデルを並列に並べた図2の一般化マックスウェルモデルを用います。
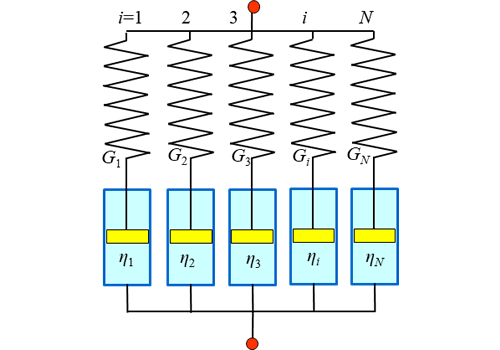
![]()
複数の2要素マックスウェルモデルのそれぞれの要素の特性を足し合わせたものが緩和弾性率G(t)になります。N個の場合の式は(5)式と(6)式です。
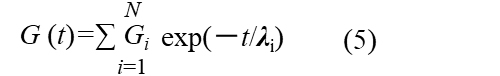
![]()
各要素の係数をうまく組み合わせることにより、図3のように所望の緩和弾性率曲線を作れ、実材料に近い特性が表現できます。なお、この手法はProny(プロニー)級数近似とよばれています。
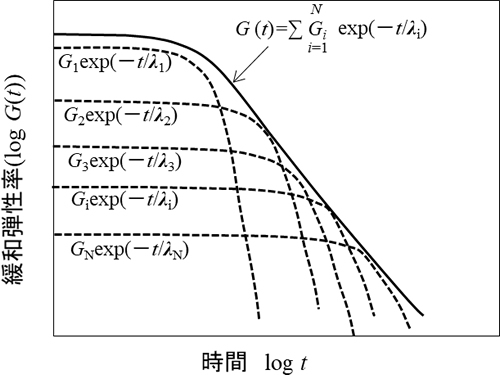
![]()
ツェナー (Zener) モデル
一般化マックスウェルモデルに並列にばね単独要素(Ge)を付加した形が図4のツェナー (Zener)モデルです。
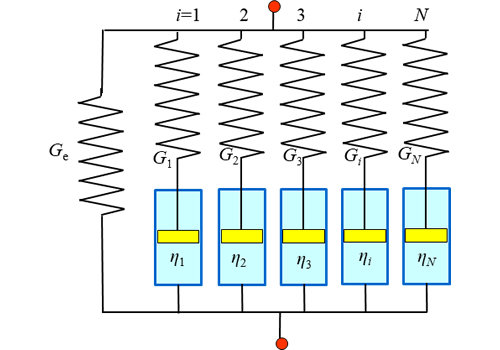
![]()
ツェナーモデルの式は(7)式、(8)式です。
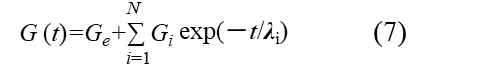
![]()
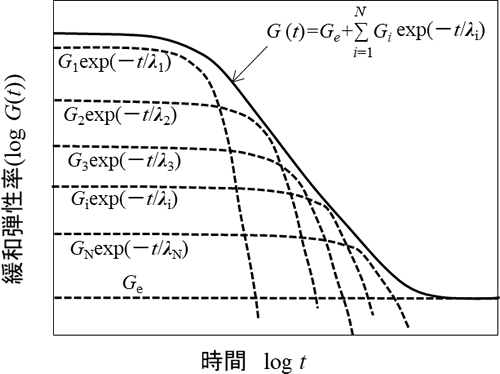
図5のように、長時間経過後に所定の弾性率に収束する特性を有する材料や条件に適用されます。
![]()
時間・温度換算則
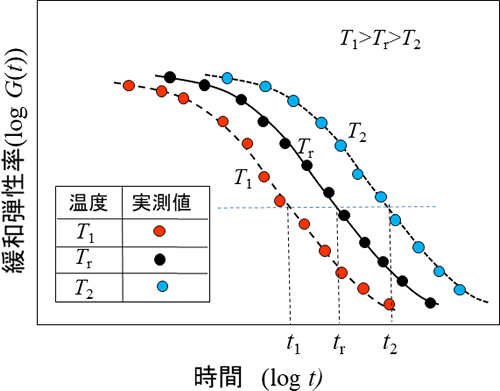
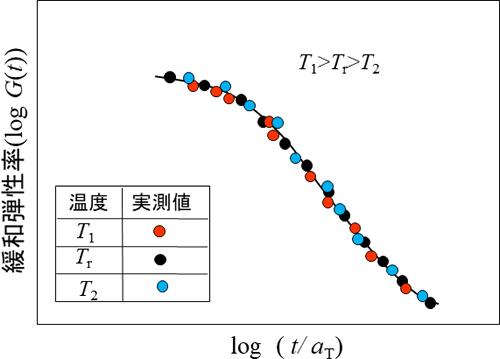
温度Tを変えてG(t)を測定すると、図6のように各温度での曲線は互いに時間軸方向に平行移動した形になることが多いようです。
![]()
温度が低いほど弾性の性質を長く保つので緩和時間が延び、曲線は右側にシフトしてゆきます。いま基準温度をTrとし、それより高い温度をT1、低い温度をT2とします。ある弾性率を選択し、そのときの時間を高い温度から順にt1、tr、t2とします。各温度での時間を基準温度での時間で除した値を時間・温度移動因子aT (T)と呼びます。ここでは次のようになります。
![]()
![]()
(9)式ではaT (T1) <1になり、T1でのデータの時間に(9)式の逆数を掛ければデータは右側にシフトし基準温度のデータに重なります。一方、(10)式ではaT (T2) >1 となり、 T2でのデータの時間に(10)式の逆数を掛けてデータを左側にシフトさせれば基準温度のデータに重なります。横軸を t/ aTにして図7のように各温度でのデータが重なれば時間・温度換算則が成立していることになり、この曲線を緩和弾性率のマスター曲線といいます。
![]()
時間・温度移動因子はWilliams, Landel, Ferryによって導かれた次のWLFモデル式がよく使われています。
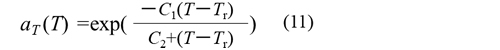

関連記事/関連ページ
●樹脂成形とレオロジー 第5回 「粘弾性体のモデル化」
●樹脂成形とレオロジー 第7回 「Die Swellの基礎と無次元数」
