樹脂成形とレオロジー 第7回「Die Swellの基礎と無次元数」
プラスチックなどの高分子溶融体は流動時に弾性の性質を示し、特にダイ末端から押し出された際に弾性回復によって膨らむことが知られています。この現象はDie SwellやBarus効果とよばれます。実際にはダイから出たあとの樹脂の冷却や重力の影響が加わりますが、ここでは非常に限定した条件での計算式を紹介します。
参考文献:J.M.Mackelvey,”Polymer Processing“,p85, Jon Wiley and Sons,Inc. New York(1962)

前提条件
(1)流出物の慣性効果、重力の影響は無視する
(2)ダイの断面形状は円形とする
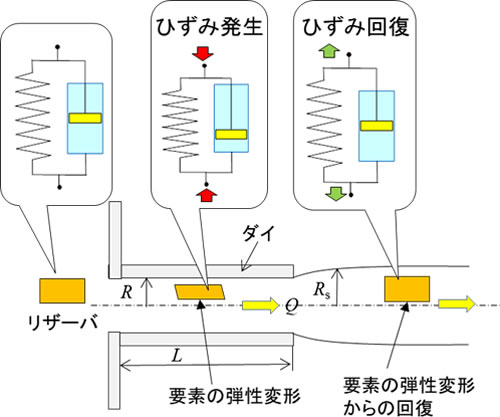
(3)樹脂は粘弾性体とし、回復しうる遅延弾性をフォークト(Voigt)モデルで表わす
(4)平均せん断ひずみは管壁のせん断応力によって発生し、フォークトモデルによって時間変化する
![]()
この前提条件で理論解析すると下の計算式が得られます。
■ダイ出口でのひずみ計算式
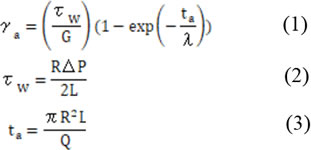

■樹脂がダイから出たあとのひずみの回復計算式
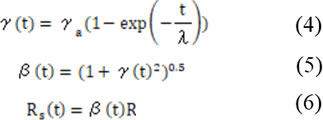

(1)式がダイ内で蓄積された最終ひずみ量で、(4)~(6)式がダイ出口から徐々にそのひずみが解放されていく状況、すなわち押出物の径の増加(Die Swell)を表わしています。
粘弾性流体の無次元数とDie Swell
流体力学では異なる実験での力学的相似性を評価したり、層流か乱流かを判断するときなどに慣性力と粘性力の比であるレイノルズ数(Re)という無次元数がよく登場します。一方、粘弾性流体特有の無次元数も存在し、Die Swellの起きやすさの指標としても使われています。ここでは後者、 Die Swellを説明します。
ワイセンベルク(Weissenberg)数:We
Weは次式で示される無次元数です。
![]()
いま、流体の粘度(η)は同じとすると、緩和時間(λ)を長くするためには弾性率(G)を小さくする方向になります(λ= η / G)。このときに(1)式の(τw/G)の Gが小さくなる寄与が大きくγaが大きくなります。すなわち、緩和時間が長くなるとひずみが大きくなるのでDie Swellが大きくなります。
一方、代表速度を管内平均流速U、代表長さを管直径2Rとすると次式が得られます。
![]()
(8)式は管壁のせん断速度(4Q/(πR³))と比例関係になっています。粘度が同じならせん断速度に比例してτwが大きくなります。すなわち、代表速度を流路の代表長さで除した値が大きくなるとγa が大きくなるのでDie Swellが大きくなります。以上からWeはDie Swellの起きやすさを予測するための無次元パラメータになっています。
Weissenbergは粘弾性体の挙動を研究したオーストリアの物理学者です。粘弾性体が回転中心の棒を這い上がる現象はWeissenberg効果として有名です。
デボラ(Deborah)数:De
Deは次式で示される無次元数です。
![]()
粘弾性体がダイ内を流れるときは観察時間はダイ内の流動時間taになりますので次式となります。
![]()
緩和時間を長くすると先に述べた理由によりDie Swellが大きくなります。またtaを小さくする方向は(3)式でQを大きくあるいはRを小さくして管壁せん断速度を大きくしますので、やはり先に述べた理由によりDie Swellが大きくなります。
以上からDeもDie Swellの起きやすさを予測するための無次元パラメータになっています。
WeとDeはそれぞれダイ断面方向と流動方向に沿う粘弾性体の通過状況に基づく無次元数と考えられます。
計算例
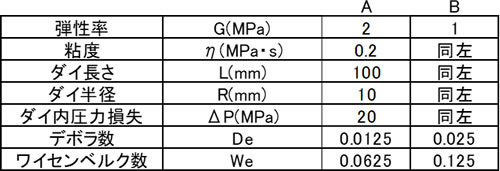
(1)式~(10)式を用いた計算結果の例を示します。条件Aと条件Bを用い、条件Bは条件Aの弾性率の半分の値にしています。図の横軸はダイから流出後の時間で縦軸は流出物の半径です。どちらの条件もダイの半径は10mmですので時間0では流出物の半径も10mmになっています。時間の経過とともに流出物の半径が広がり飽和していく状況が示されています。条件BではAよりDe数もWe数も大きくなり、Die Swell量も多くなっています。実際の材料の粘弾性特性は非常に複雑で、ダイから出た後の樹脂の冷却や重力の影響などが加わるため、予測にはいろいろな経験式の導入も必要です。プラスチックの押出成形やブロー成形ではDie Swellが生じた後に製品の最終形状が決まりますので、ダイの最適設計や成形条件の選定を合理的に行うにはCAEシミュレーションの活用が効果的です。
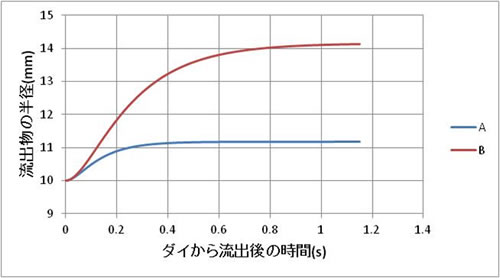
![]()
De数の自然現象への適用例
ここでは氷河の移動について簡単な計算をしてみます。
下式を用います。
![]()

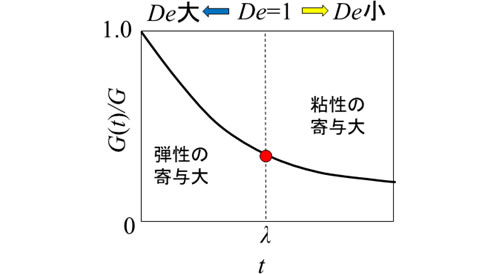
De≪1で液体とみなせる。
De≫1で固体とみなせる。
De=1で弾性と粘性の寄与が同等
氷河はλ=10⁵sといわれています。(9)式でDe数を計算してみます。
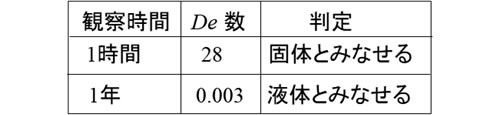
観察時間1時間ではDe=28となり De≫1 なので固体とみなせます。この時間では動いているようには見えませんのでそうなります。
観察時間1年ではDe=0.003となり De≪1で液体とみなせます。1年経つと明らかに動いていますのでそうなります。どんな物体でも観察時間を長くすると動いています。

トリビア(豆知識)
デボラ数の提唱者は国際成形加工学会(PPS) 設立者のJ.L.White教授です。デボラは旧約聖書に登場する女性預言者で「山々は主の前に揺れ動いた」と歌いました。White教授は、デボラはタイムスケールの最初の理解者であるとして「デボラ数」と命名しました。
人間の一生というタイムスケールでは、山が揺れ動くという現象は観察できませんが、主は山々が動いて海に入る様子を悠々とご覧になられるとデボラは歌っています。まさにパンタレイ ( = Everything flows,, 万物流転 ) です。
関連記事/関連ページ
●樹脂成形とレオロジー 第6回 「緩和弾性率の表わし方と時間・温度換算則」
●樹脂成形とレオロジー 第8回 「流体の分類」
