OpenFOAMで回転を表わす４つの方法 │ DISCOVER CAE

OpenFOAM で回転を表わす４つの方法

流体計算の対象として、食品材料の撹拌や船のスクリュー、電子機器の空冷ファンなど、回転機構が含まれているものは多くあります。ここではOpenFOAMで回転を扱うための４つの方法を紹介します。

rotatingWallVelocity境界条件

回転している物体が回転対称である場合にはrotatingWallVelocity境界条件を用いることができます。

実際の物体が回転すると（滑りなし条件によって）物体表面に接触している流体が（同じ速度で）引きずられるように運動しますが、この境界条件はそれを表すことが出来ます。

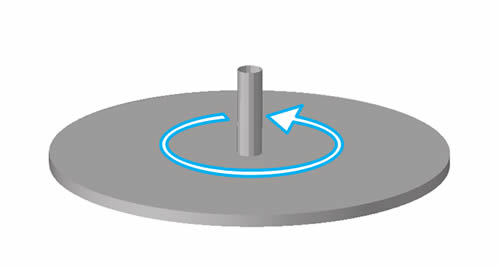
図１に適用可能な物体形状の例を示します。形状が回転対称の回転皿であるため、この境界条件で回転が実現できます。

Single Rotating Frame（SRF）系ソルバー

回転座標系で物体が静止しているような系であれば、回転座標系で流体方程式を解くことでメッシュを回転させることなく計算が可能です。

それを実行するのがSRFSimpleFoamとSRFPimpleFoamです。

前者は定常計算用ソルバーで、後者は非定常計算用のソルバーです。

これらのSRF系ソルバーは解くべき流体の方程式に遠心力とコリオリ力の効果を追加することで、回転座標系で見た流体の運動を解きます。この場合、回転している物体が回転対称である必要はありません。

図２にSRF系ソルバーを適用可能な例を示します。この例では解析空間が円柱形なので、プロペラと同速度で回る回転座標系ならプロペラが静止した状態で計算することができます。

Multiple Reference Frame機能

ここまでは回転する物体のみが存在する場合の計算方法でしたが、容器内の撹拌など解析対象の一部だけが回転する場合は、Multiple Reference Frame(MRF)機能を用います。これにより、回転部分を包む一部領域を回転座標系で考え、それ以外を静止しているとすることでメッシュを動かさずに計算することが可能です。

容器内に回転子がある流れの２次元問題のモデル図と計算結果を図３に示します。回転子を含む中央の円柱領域を回転座標系で考えることで回転子を動かすことなく回転の計算を行っています。

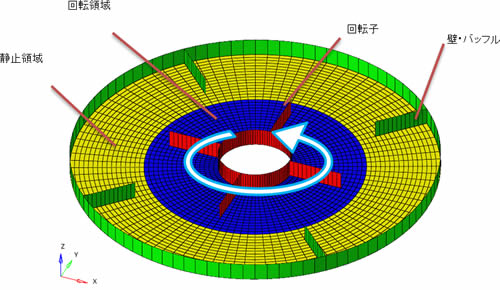
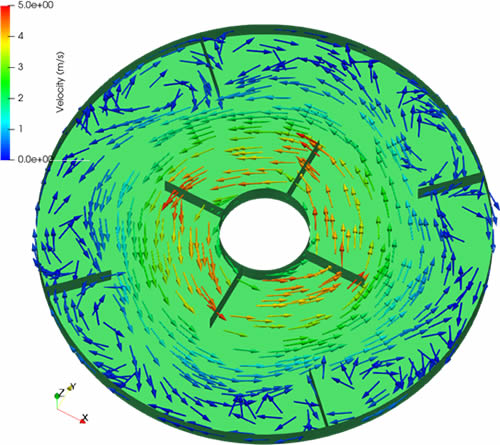
MRFはsimpleFoamやpimpleFoamなど多くの種類のソルバーで実行できる上に、解析対象全体を回転座標で考える必要がないため、解析空間の形状が図３のように回転対称性をもたない場合でも計算できます（図３のケースでは容器にバッフルがあるので回転対称性がありません）。つまり、幅広い対象に適用できるという利点があります。

ただ、静止領域が回転対称でない場合、静止領域に対する回転体の相対位置がMRFでは変化しないなど、計算が実現象と乖離する部分もあります。

よって、解析結果の精度が望む程度得られているかどうかには確認を要します。

Sliding Mesh

MRF機能で望む計算精度が得られなかった場合、メッシュ移動の機能を用いて回転体を実際に回転させて計算することが考えられます。

メッシュを回転領域と静止領域に分け、回転領域を剛体回転させることで回転を再現します。

この際回転領域と静止領域はSliding Meshで接続されます。

図２にメッシュ回転を利用した計算例を示します。メッシュを回すことで直接容器内の流体の撹拌の非定常計算を行っています。撹拌の様子を見るために粒子追跡機能を用いた可視化を行っています。

この方法は他の３つの方法と比べてメッシュ移動が伴う分計算負荷が高いことが難点です。