樹脂成形とレオロジー 第11回「 非凝集系懸濁液の粘度」
プラスチックは軽量で加工しやすい特徴がありますが、単体のみでは工業界の要求に応えるのが難しいことが多く、特定の材料を混ぜ込んで性能を高める工夫がなされています。

プラスチックに特定の材料を混ぜ込む目的には、強度、放熱性、遮音性、摺動性の向上や導電性・磁性の付与などがあり、主にガラスやカーボンなどの無機材料が用いられ、充填剤やフィラーとよばれています。充填剤の量が増えれば目的の機能は向上しますが、樹脂は流動しにくくなり、成形が困難になるという問題が生じるため、適切な配合量を選択することが重要となります。ここでは充填剤量と粘度の関係についての基礎を説明します。
混合液の分類
固体粒子が液体中に分散している系を懸濁液(サスペンション)とよび、非相溶の液滴が液体中に分散しているものを乳濁液(エマルジョン)とよんでいます。充填剤入りの溶融樹脂は懸濁液に該当します。
固体粒子の大きさ、形状、分布、配合量などで流動挙動が大きく異なります。粒子間力が引力として働く場合は粒子は数珠のように連なった凝集状態になり、挙動はさらに複雑になります。
ここで紹介する懸濁液は凝集のない球形の単分散粒子からなり、粒子間に剛体反発のみが働く理想的な状態を仮定したものです。
粘度式の変遷
(1)低濃度系の基礎理論式(Einsteinの式)
懸濁液のレオロジー的性質についての理論解析は、剛体球の低濃度懸濁液の粘度に関するEinsteinの古典的研究に始まりました(1906年)。この摸型は無限に広がった流体中の単純せん断流動場に置かれた、孤立した一個の球からなっています。彼は粒子と流体の相互作用の影響を考慮し、クリープ流動域(慣性力が無視できる非常に遅い流れ)のNavier-Stokesの式と連続の式から次式を導きました。
![]()
ここで、 ηs :懸濁液粘度、 η0 :溶媒粘度、 φ:粒子の固体体積分率(体積濃度)です。上式は溶媒中の粒子の占める体積が増えると懸濁液の粘度はそれに比例して増加することを示しています。 ηs を η0 で除した値は溶媒に固体を分散させた懸濁液がもとの溶媒の粘度の何倍になるかを表す指標となり、比粘度とよばれます。比粘度を ηr とすると次式の形になります。
![]()
(2)高濃度系への拡張-1(Simhaらの式)
Einsteinの理論は、粒子間の相互作用が無視できるごく低濃度の懸濁液に限られていました。Simhaらは球間の相互作用を考慮し、次式を導きました。
![]()
これは比粘度が固体体積分率の二乗に比例する形であり、固体体積分率が大きくなるとEinsteinの式よりも粘度が上昇します。
(3)高濃度系への拡張-2(Mooneyの式)
高濃度系の本格的な粘度式の導出はMooneyによりはじめて試みられました。彼は、球形粒子を溶媒の中に順次加えていくときの粘度の増加分は、それまでに投入した粒子体積を除いた液について起きるとし、この自由容積が徐々に減少することを考慮して次式を導きました。これは指数関数であり、固体体積分率が大きくなると急激に比粘度が上昇します。
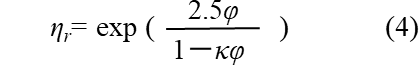
ここで、κ:クラウド係数であり、粒子の最大体積分率をφmとするとκ=1/φmとなります。粒子がすべて同じ大きさの球とすると六角格子配列の理論式からφm=0.74となります。Mooneyの式は低濃度ではEinsteinの式と一致し、φの増加とともにηrが大きくなり、φ=φmで∞になります。この式は現在でも高濃度懸濁液の粘度予測に広く使われています。なお、球形以外の粒子形状にも適用するときは次式の形も用いられます。 KEは粒子形状に依存する係数です。
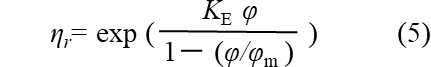
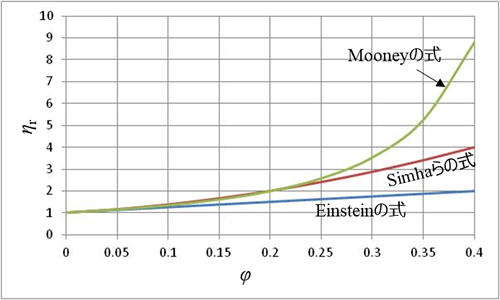
各予測式の比較を図1に示します。適用範囲としてはEinsteinの式ではφ=0.1程度まで、Simhaらの式ではφ=0.3程度までです。これを超えるとMooneyの式が比粘度は非常に大きくなります。なお、ここでは粘度のせん断速度や温度依存性は触れていませんが、ある特定のせん断速度や温度に揃えたときの比較という前提になります。
この他にも数多くのモデル式があり、楕円や棒状(ファイバー)粒子などに適用できるモデルも提案されています。

関連記事/関連ページ
●樹脂成形とレオロジー 第10回 「粘度の温度依存性の表わし方」
●樹脂成形とレオロジー 第12回 「気泡成長の基礎」
●OpenFOAMの粘性モデル