樹脂成形とレオロジー 第12回「 気泡成長の基礎」
プラスチックの成形加工の分野の一つに発泡成形があります。これは溶融樹脂中で気泡を成長させ、成形品に衝撃吸収性、クッション性、断熱・保温性、吸音・遮音性などを付与するとともに、軽量化を図ることを目的としています。ここでは、気泡の成長解析の基礎式と簡易計算例の説明を行います。

基礎式の誘導
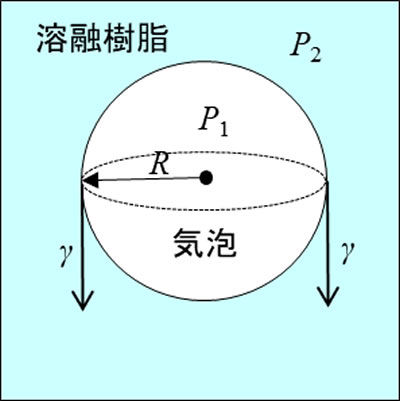
図1のように溶融樹脂中に小さな球体の気泡が一個存在している場合を考えます。ここで、P1:気泡を膨張させるための内部圧力、P2:気泡の膨張を抑える外部圧力、γ:気泡の膨張を抑える樹脂表面張力、R:気泡半径です。
![]()
まず、表面張力により膨張を抑える力をFsとすると、次式が成立します。
![]()
圧力差により膨張しようとする力Fpは次式となります。
![]()
よって、膨張する力Feは次式となります。
![]()
![]()
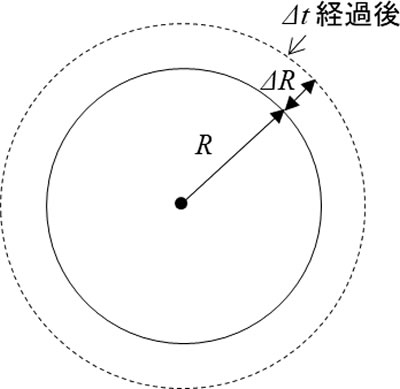
次に、図2のようにΔt経過後に膨張により半径がΔR大きくなった状態を考えます。これにより生じる樹脂側のひずみεは次式となります。
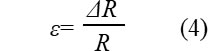
![]()
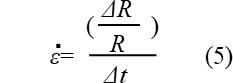
発生応力σは樹脂粘度をηとして次式となります。
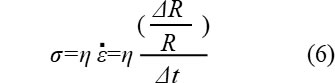
σに円の表面積を掛ければこのときに樹脂側が気胞膨張に反発する力Frが計算できます。
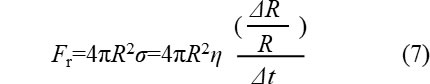
(3)式のFeと(7)式のFrが釣り合うので、整理して次式が得られます。
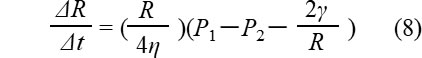
微分形式にすると次の一般式が得られます。
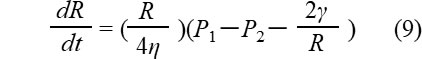
(9)式が文献などでよく見られる気泡の成長式になります。
簡易計算例
いま、気泡膨張のための内圧P1 が外圧P2 に比べて非常に大きいとします。P1 ≧P2 のとき(9)式は次式となります。
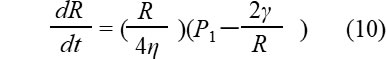
ここで、気泡の体積をV 、温度をTとして簡易的にボイルシャールの法則を適用すると次式となります。
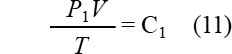
気泡を球体とすると体積は次式となります。
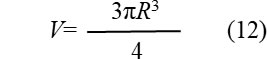
(11)、(12)式より次式が得られます。
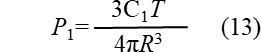
(13)式を(10)式に代入して次式が得られます。
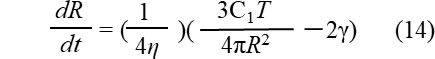
気泡の成長が終わるときは次式が成立します。
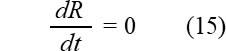
このとき次式が得られます。
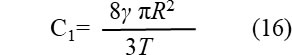
ここで、γ =0.0725N/m (水の値、エポキシ樹脂もこれに近い)、T=160℃(433K)において最終気泡径R=0.2mm(2.0E-4m)としてみます。これらを用いると、 C1 =5.625E-11Nm/Kとなります。本簡易計算ではC1をこの値に固定します。
なお、現実には化学発泡のように初期は気泡がない状態や、物理発泡では成形機内で高圧で圧縮されて非常に小さいサイズになっていますが、ここでは計算の簡略化を図るために、初期半径R0=0.05mmとし、温度と粘度の影響を調べることにします。また樹脂部は実際には気泡成長により円周方向に引っ張られ、半径方向に縮む2軸伸長流動に近い状態になっていますが、非常に複雑なので、ここでは粘度はせん断と伸長の区別はしないようにしておきます。
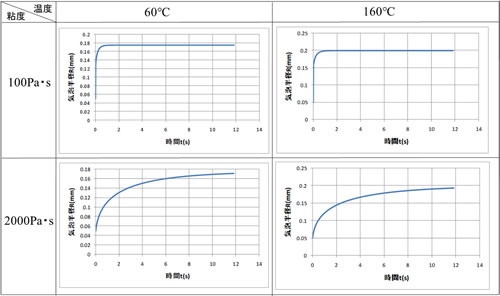
温度2水準と粘度2水準を組み合わせた計算結果を図3に示します。横軸は時間、縦軸は気泡半径です。同じ粘度なら温度が高い方が最終気泡径が大きくなります。すなわち、よく発泡します。同じ温度なら粘度が低い方が短時間で最終気泡径に達し、粘度が高いと飽和までに時間を要しています。ここに示した気泡の成長計算は気泡一個が自由に膨張できるという前提ですが、実際のプラスチック成形加工プロセスでは無数の気泡が発生するので、気泡同士あるいは各気泡の周りの樹脂の干渉が生じ、解析は非常に難しくなります。ただし、気泡成長のシミュレーションに関する多くの論文は(9)式を基礎として、その上に改良を加えています。
関連記事/関連ページ
●樹脂成形とレオロジー 第11回 「非凝集系懸濁液の粘度」
●樹脂成形とレオロジー 第13回 「熱硬化性樹脂成形と物性値の変化」
●ウレタン発泡流動解析 パラメータ検証実験
●OpenFOAMによる自動車シートの発泡成形解析