CAE解析業務の基礎講座[6] ~シンプレックス法~
今回はシンプレックス法の説明です。
第6回 シンプレックス法の概要
前回の基礎講座では、エクセルの分析ツールを使って実験データと任意の数式との誤差が最小になる様に、数式内の未知パラメータをフィッティングする方法について説明しました。今回は、フィッティングの基本となるシンプレックス法について簡単に説明します。
1. はじめに
シンプレックス法は一般的な線形計画問題を解くアルゴリズムで決定論的な手法の一つになります。未知パラメータがn個の時、n+1個のデータでシンプレックスを作成します。
例えば、未知パラメータが2個の時、3個のデータでシンプレックスを作成します(←3個なのでシンプレックスは三角形)。三角形の頂点のうち、残差が最も大きい頂点を残差が小さくなる方向に移動させ、新しい三角形を作成します。次に残差が大きかった頂点を移動させ、次々と三角形を更新して、解を求めます。
2. 例題の説明
未知パラメータ2が個の場合を例に、具体的な計算手順を説明します。
式(1)に示す計算式中の2つの未知パラーメータdとeをシンプレックス法を使って求めます。
![]()
ここで、Tは温度を示します。
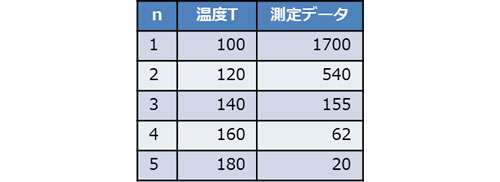
温度を変更して測定したt0のデータは、5個(n=5)あるとします(表1参照)。
![]()
d、eの残差Sを以下の式で求めます。
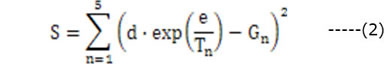
ここで、Tnはn番目の測定温度、Gnは測定データになります。
解空間Sのイメージを図2に示します。
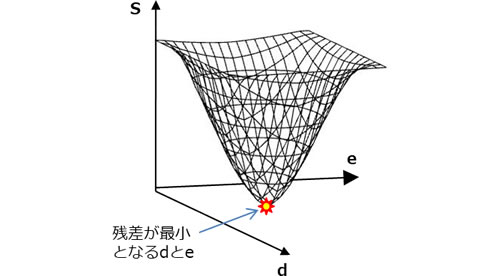
![]()
3. 操作手順
具体的な操作手順を説明します。
ステップ① 未知パラメータd,eの任意の初期値pを、未知パラメータの個数+1個仮定します。
今回は未知パラメータ2個なので、初期値を3個定義します。
p1=(d1,e1) 、p2=(d2,e2) 、p3=(d3,e3)
ステップ② ステップ①で仮定したp1、p2、p3を使って、残差Sを計算します。
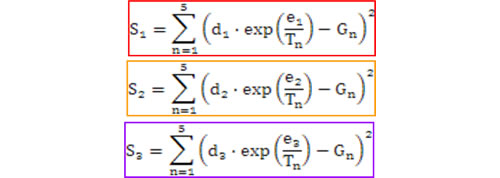
ステップ③ ステップ②で計算したS1~S3を、解空間上にプロットし、三角形(シンプレックス)を
作成します。
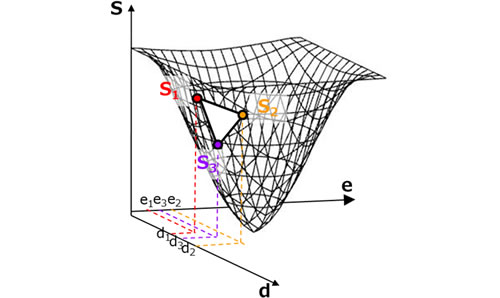
ステップ④ S1、S2、S3の中で、最小(=最も解に近い)と最大を特定します。今回の例では
最小がS3で、最大がS1になったとします。解は最大であったS1の逆方向に存在す
ると仮定し、S1の移動方向をS2とS3から求めていきます。
ステップ⑤ 最大であったS1を除いたS2とS3の未知パラメータdとeの重心dAVE, eAVEを求めます。
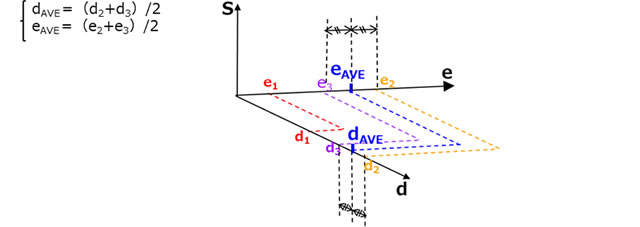
ステップ⑥ 最大のd1を、ステップ⑤で求めた重心dAVE方向に移動し、新しいdnewを定義します。
同様に、e1wもeAVE方向に移動し、新しいenewを定義します。
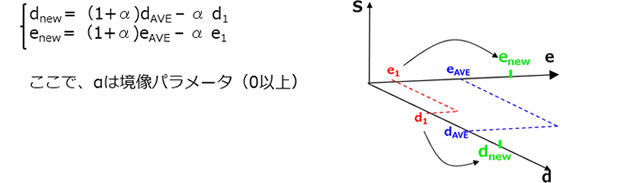
ステップ⑦ ステップ⑥で求めたdnewとenewを使って、仮の値Snewを計算します。
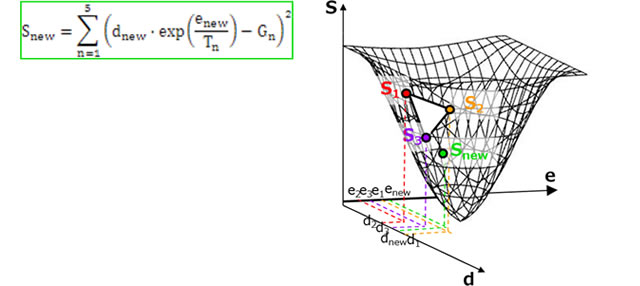
ステップ⑧ ステップ⑦で求めたSnewに対する最小S3と最大S1の大小に応じて、新しい
d4,e4を求め、S4を算出します。
まず、 Snew < S3のとき、以下の式からdnew2とenew2を求め仮の値Snew2を計
算します。
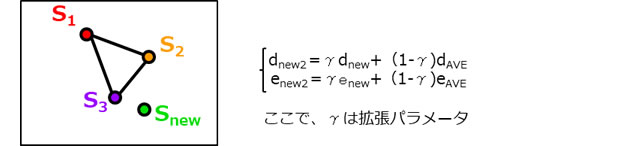
Snew2がSnew より小さい場合、 dnew2とenew2を正式にd4とe4とし、Snew2もS4
として新しいシンプレックスを確定します。
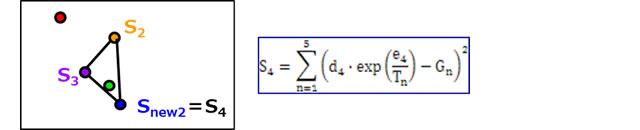
Snew2がSnew よりかえって大きくなってしまった場合、 dnew2とenew2は使わず
に、 dnewとenewを正式なd4とe4とし、SnewもS4として新しいシンプレックスを
確定します。

可能性として存在するSnew が最大とS1より大きくなってしまった場合は、以下
の式を使ってd4とe4を計算し、S4を算出します。

ステップ⑨ 以降、ステップ④から⑧を繰り返してシンプレックスを移動させ、最小とな
るdとeを求めます。
参考資料:http://aoki2.si.gunma-u.ac.jp/LaTeX/simplex.pdf
関連記事/関連ページ