樹脂成形とレオロジー 第16回「 Kamalの反応速度モデル」
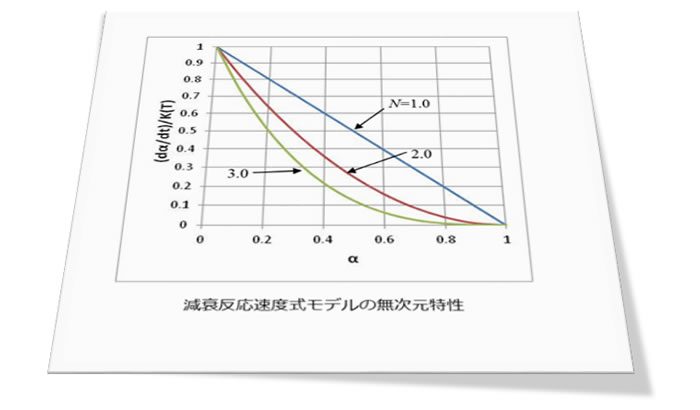
前回は等温状態で初期に反応速度が最大になる減衰反応速度式を紹介しました。実際の熱硬化性樹脂は用途に応じて非常に多くの素材が配合されるのが一般的であり、反応形態が異なる多くの材料が存在します。したがいまして、等温状態で反応速度が初期に最大にならない特性の材料があり、これをうまく表す反応速度式が望まれます。これに適合するモデルの一つがKamalの反応速度式であり、現在ではCAEの世界でもっとも頻繁に使われています。
1. Kamalモデルと基本特性
Kamal モデルを下記します。
![]()
![]()
![]()
ここで α:反応率、t:時間、T:温度、dα/dt:反応速度、K1, K2:温度の関数となる係数、N, M, Ka, Ea, Kb, Eb :材料固有の係数です。
(1)式は次の形になります。
![]()
右辺第一項は前回ご紹介した減衰反応速度式になります。右辺第二項はα=0と1で反応速度が0で、等温状態ならα=M/(M+N)のところで最大反応速度となる特性を持たせています。
(4)式をK1で除すると次の無次元反応速度の関係式が得られます。
![]()
ここで、次のように定義します。
![]()
![]()
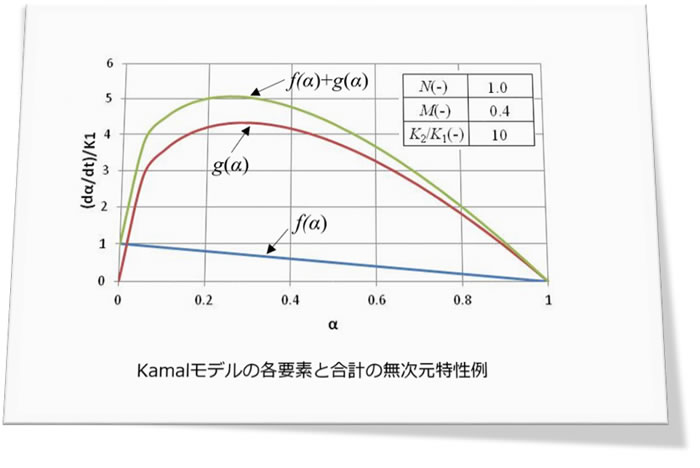
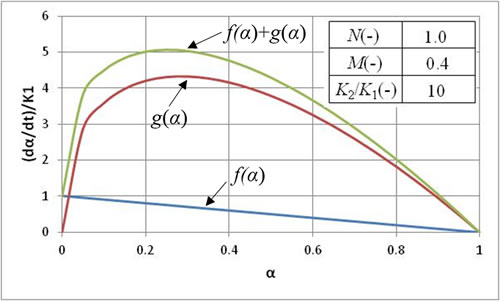
図1に f(α), g(α) とその合計の特性例を示します。f(α) は初期値が1でα の増加とともに値が減少し、α=1 で0となります。g(α)はα=0と α=1で値が0となり、その間で最大値が生じます。 f(α) と g(α) を足し合わせたものがKamalモデルとしての無次元特性となります。すなわち、減衰反応速度式をベースラインとして、その上に反応途中で反応速度が最大になる速度式を乗せたモデルとなっています。
![]()
2. 反応速度、反応率の時間変化
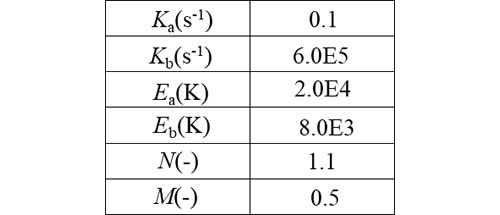
ここでは表1のように係数を固定して特性を調べてみます。
![]()
2.1 等温特性例
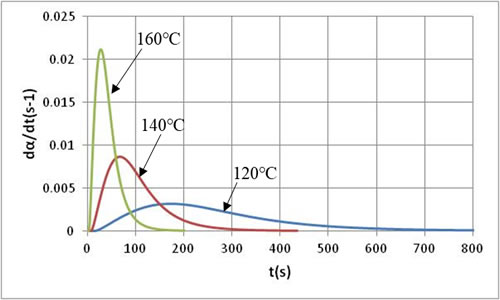
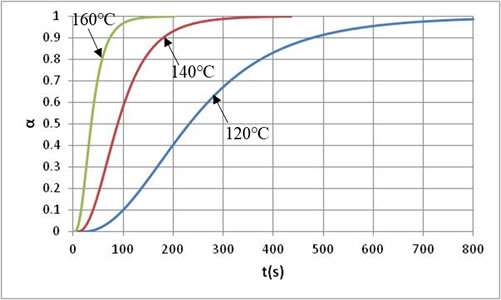
まず、温度をパラメータとし、それぞれの温度に保った場合の特性を比較します。図2は反応速度の時間変化で、前回ご紹介した減衰反応速度式とは異なり、反応開始後しばらくして反応速度の最大値が生じます。温度が高いほど反応速度の最大値は大きくなり、時間の経過とともに急速に減衰していくことがわかります。温度が低いと反応速度の最大値は小さいですが、時間をかけて減衰していく特性となります。図3は反応率の時間変化で、温度が高いほど反応が急激に進み、短い時間で反応が終了していることがわかります。
![]()
![]()
2.2 昇温特性例
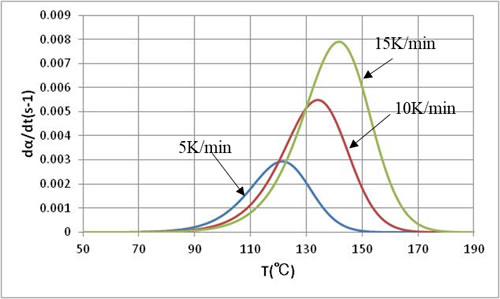
図4に、昇温過程における温度と反応速度の関係を示します。昇温速度が遅いと発熱のピーク温度が低く、昇温速度が速くなるとピークが高温側にずれ、ピーク自体の値も大きくなります。この傾向は前回ご紹介した減衰反応速度式の場合と類似しています。
![]()
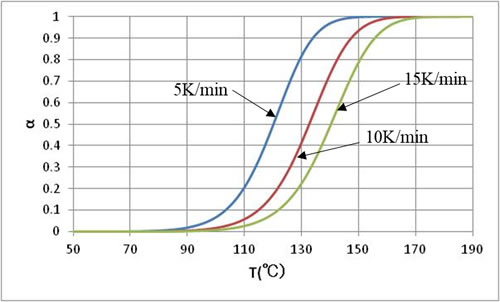
図5に、昇温過程における温度と反応率の関係を示します。昇温速度が遅いと低い温度で反応が終了し、昇温速度が大きくなると反応終了温度が高温側にシフトします。この傾向も減衰反応速度式の場合と類似しています。
![]()
3. その他の反応速度モデル
減衰反応速度モデルやKamalモデルでは反応速度プロファイルが決まった形になりますので、複数個所で反応速度のピークが生じるような場合には対応しにくくなります。このときは複数の減衰モデルあるいはKamalモデルの組み合わせで表現する1)か、あるいは自由な形の実験式として表すModel-Free Kineticsとよばれる手法2) があります。前者はかなり煩雑な作業が必要になります。一方、後者は特定条件でうまくフィッティングできたとしても、条件が変わると合いにくくなる場合が多く、取り扱いや適用範囲などに注意が必要です。
参考資料:
1) サイエンス&テクノロジー社編:樹脂の硬化度・硬化挙動の測定法と評価方法, 223(2007)
2) M.R.Kessler and S.R.White: Journal of Polymer Science: Part A:Polymer Chemistry,40, 2373 (2002)
関連記事/関連ページ