樹脂成形とレオロジー 第19回「 伸長粘度の測定法と特性例」
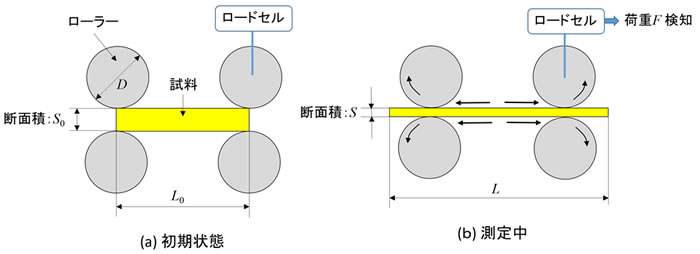
一軸伸長粘度の測定原理
もっとも初期に検討された方法は、Meiβner法とよばれる一軸引張法です。現在ではこれに変わる色々な方法がありますが、原理を説明しやすいので、ここではMeiβner法を例に説明します。図1にMeiβner法の測定原理の模式図を示します。(a)は初期状態で、一定間隔に配置された直径Dのロール間に試料をはさみます。初期の試料の長さはL0, 断面積はS0です。 (b)は測定中の状態で、ロールを回転させて試料を引き延ばします。試料の長さはL,断面積はSになっています。また、試料を変形させるのに要した力Fが測定されます。このときのロールの回転数をNとすると回転速度vは次式となります。
ひずみ速度
は(2)式となります。
一軸伸長粘度ηEは次式で求められます。
ここで、σ：引っ張り応力、F：発生する力、S：試料断面積です。(3)式の右辺でFは測定値、は(1),(2)式に設定条件を代入して求められますので、Sが分かればηEが求められます。測定試料は高分子溶融流体であり、測定中は体積変化はないとみなせます。したがって次式が成立します。
ひずみεは大変形ですので対数ひずみを用いた次式となります。
なので次式が得られます。
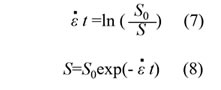
(8)式により時刻tのSが計算できますので、これを(3)式に代入してηEが求められます。閉じた空間内に試料を満たして行える単純せん断粘度の測定に比べ、解放された空間で溶融体を取り扱う一軸伸長粘度の測定はなかなか難しいようです。
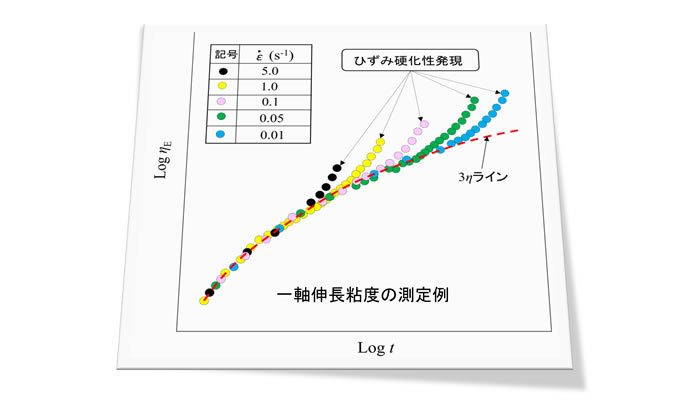
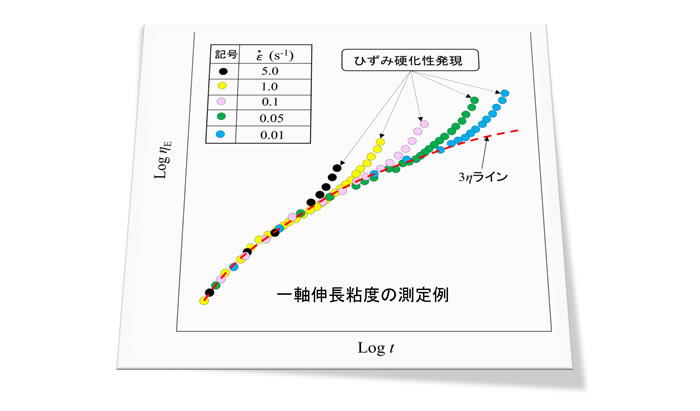
一軸伸長粘度の測定例
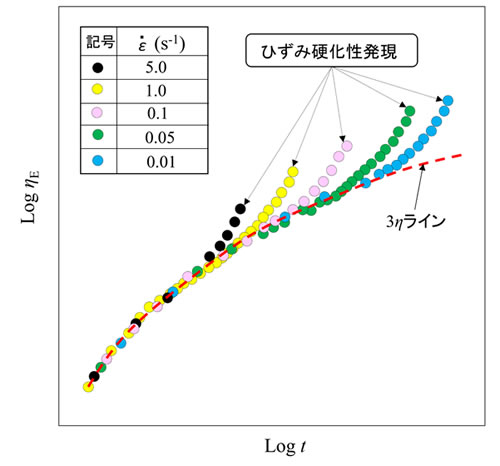
１軸伸長粘度の測定例を図2に示します。横軸、縦軸はそれぞれ時間tと一軸伸長粘度ηEを対数で表しています。各記号はそれぞれ一定のひずみ速度で試料を伸長させたときの特性を示しています。ひずみ速度が大きいほど短い時間で測定が終わります。ηEは時間の経過とともに値が増加する特性を持ちます。図では測定の後半に急激にηEが増加しています。この特性は例えばブロー成形において、パリソン(成形中に空気を吹き込んでパイプ状にした樹脂形状)が破れないように、分子鎖に枝分かれを設けるなどして、伸びて薄くなったところが硬くなる「ひずみ硬化」と呼ばれる現象が起こるようにしてあるためです。ひずみ硬化性は緩和時間の長い超高分子量成分や分子に分岐成分があると発生しやすくなります。一方、フィルム成形ではひずみ硬化性が大きい場合は高引張速度になると分子間の絡まり合いが顕著になり、成形中の溶融破断が起こりやすくなることがあります。ひずみ硬化性がない樹脂の場合は測定の後半にηE は飽和します。
経過時間の短い領域では、データが重なり、ひずみ速度には依存しない特性を示しています。一方、赤の破線はせん断粘度ηの3倍の値のラインになり、これが重なったデータの上に乗ります。これはひずみ速度に依存しない領域は、微少変形での粘度の値と対応しているためです。ηEがηの3倍になる理由は前回ご説明しました。
射出成形などのCAEではひずみ硬化や粘度の時間依存性は通常取り扱いませんが、ブロー成形ではこの特性が重要になります。したがって、ブロー成形用CAEでは図2の樹脂特性をうまく取り扱うためのモデル式を用います。
次回はその内容を説明します。
関連記事/関連ページ