樹脂成形とレオロジー第21回「K-BKZモデルでの伸長粘度の計算例」 │ DISCOVER CAE

樹脂成形とレオロジー第21回「 K-BKZモデルでの伸長粘度の計算例」

K-BKZモデル

前回、粘弾性体の一定ひずみ速度での一軸伸長粘度計算式ならびに単純せん断流動での粘度の計算式を示しました。ここでは現象をできるだけ単純化するために、次の仮定を設けることにします。

①時刻0から応力が発生する
②緩和モジュラスと緩和時間は一組だけの組み合わせとする

このときの式は下記のようになります

一定ひずみ速度での一軸伸長粘度計算式

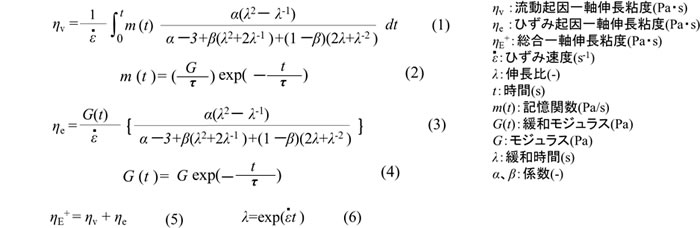
参考：単純せん断流動での粘度の計算式

計算前提

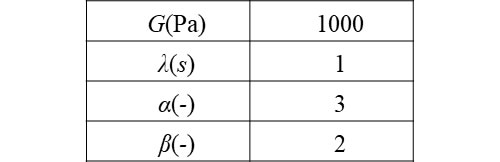
表1に計算に用いた係数の値を示します。これらを用いて3水準のひずみ速度のときの一軸伸長粘度の特性を比較しました。また、せん断粘度との比較も行いました。

一軸伸長粘度の計算結果

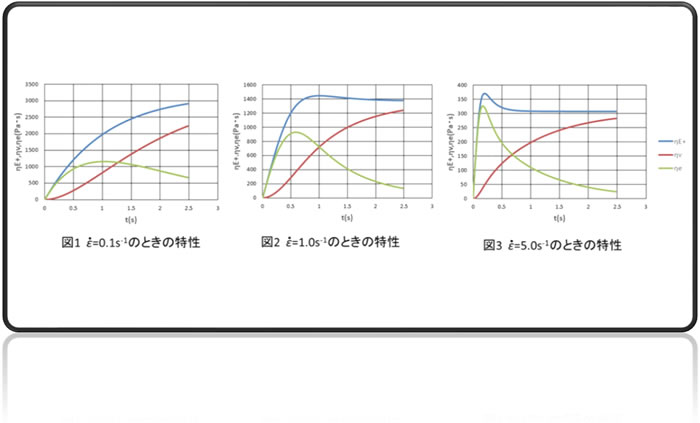
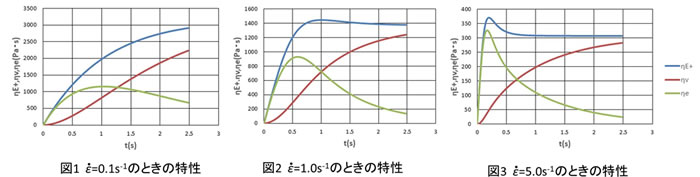
図1にひずみ速度=0.1s ^-1のときの特性を示します。η_vは流動起因一軸伸長粘度、η_eはひずみ起因一軸伸長粘度、η_E⁺はその足し合わせの総合一軸伸長粘度です。時間の経過とともにη_vは増加します。これは(1)式に示したようにη_vは積分型の式で求めるようになっており、過去の履歴の積み重ねのためこのような増加曲線になります。一方、η_eは1s付近でピークを持つ変化をします。これはη_eを求める(3)式は減少特性を持つG(t)と増加特性を持つλの項との掛け合わせになっており、G(t)の減少がゆるやかな初期ではλの項の増加の寄与が大きくη_eは増加します。その後、時間の経過とともにG(t)が大きく減少していくため、 λの項が増加してもη_eは減少していきます。したがって、途中にピークが生じる形となります。前回ご説明しましたように、常に試料が形を変える伸長流動下では、流動起因の発生応力とその時点でのひずみ起因の応力の合計が総合応力になります。(1)式、(3)式はそれぞれの応力をひずみ速度で除して粘度の単位にしたものです。したがいまして、(1)式で得られるη_vと(3)式で得られるη_eの足し合わせが総合一軸伸長粘度η_E⁺になります。図1ではη_E⁺は時間とともに増加しますが、変化率が小さくなる飽和型の曲線の形になっています。

図2に=0.1s ^-1のときの特性を示します。ひずみ速度が大きくなると粘度が低くなります。η_E⁺はη_eの急激な増加と減少により途中でピークができる形に変わってきます。=5.0s ^-1のときの特性を示します。さらに粘度が低くなり、η_E⁺は初期のピークの形が顕著になります。

一軸伸長粘度とせん断粘度の比較

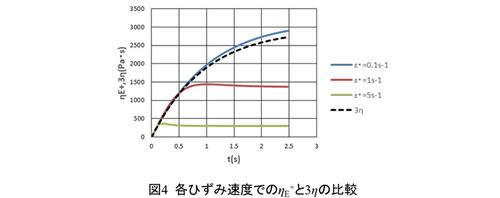
図4に各ひずみ速度でのη_E⁺の時間変化を並べました。また、(7)式で計算される単純せん断流動での粘度ηの3倍の値を重ねました。ここではせん断速度=0.1s ^-1にしてあります。ひずみの小さい初期時刻で一軸伸長粘度はせん断粘度の3倍の値に一致しています。本講座第18回「伸長流動について」で非圧縮性のニュートン流体では一軸伸長粘度はせん断粘度の3倍の値になることを説明しました。図4の結果は粘弾性流体においてもこれが成り立つことを示しています。

ここでは緩和スペクトルの本数は1本としましたが、この本数の増加とα、βの組み合わせ方で、いろいろな形ができ、実測値に近い特性にできます。そして、決定された係数を用いて、ブロー成形などの二軸伸長の現象の解析に進みます。ただし、まだ、ひずみの表示法などに不十分な点があるとして式の改良の検討も進められています ¹⁾。

参考文献
1)高橋雅興：成形加工, 17,467(2005)

樹脂成形とレオロジー 第21回「K-BKZモデルでの伸長粘度の計算例」

樹脂成形とレオロジー第21回「K-BKZモデルでの伸長粘度の計算例」