Mat. Curve Modeller:
遅れて来たもう一つの材料データ作成ツール – 5
最適化ツールの機能の向上と相まって、非線形材料データの作成方法、検証方法は多くの研究者、企業からの提案があり、商品化もされています。弊社でも、独自の視点を形にした材料データ作成ソフトMat. Curve Modellerを2021年11月にリリースしました。以下に、開発者によるコラムをお届けします。
前回より、Mat. Curve Modeller のMises⇔SAMP変換機能に焦点をあてて解説しています。今回はその2回目です。少しだけ数式が出てきます。

構成則によって、入力するSSカーブは異なる
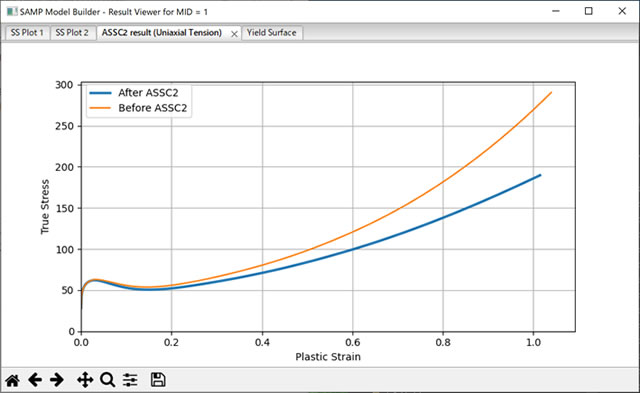
最初から疑問を抱かせるようなサブ・タイトルですが、本当です。特に不思議なことではありません。構成則によって、入力するSSカーブが異なる例を図1を示します。ここで、”Before ASSC2”というラベルのグラフは等方性弾塑性材料(Mises構成則)用に作成したSSカーブ、”After ASSC2”というラベルのグラフは樹脂材料用の等方性弾塑性材料SAMP用に作成したSSカーブです。ポリカーボネート材の引張試験結果をシミュレーションで再現するために、それぞれの構成則に合わせてSSカーブを作成しましたが、SSカーブは異なっています。
ここに示した2つのSSカーブが異なる原因は変形に伴う体積変化の考慮の有無によるものです。Mises構成則における塑性変形では体積は変化しませんが、樹脂材料用の等方性弾塑性材料SAMPでは、塑性変形に伴う体積の変化を考慮可能です。図1の樹脂材料用の等方性弾塑性材料SAMP用に作成したSSカーブは、樹脂材料が引張の塑性変形に伴い体積が増加することを前提としています。

弾性変形時の真応力
手始めに、等方性弾性体の真応力の式を導出してみましょう。図2に示すように、1片が L0 の立方体の左右の面を引張り、立方体を1軸引張状態とします。ここでは、左右の方向をX軸と一致させて考えます。公称ひずみ(εn)を使えば、変形途中の直方体の各辺の長さは図2に示すように表現できます。
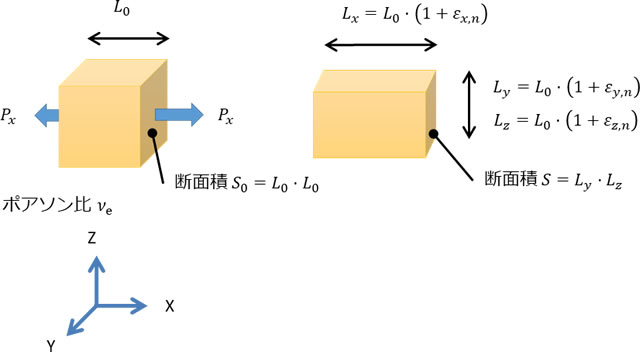

真応力は変形途中における荷重と断面積の比です。真応力を求めるため、変形途中の断面積を考えます。変形途中の断面積は公称ひずみを使って、式1のようにあらわされます。
![]()
この式を引張方向の真ひずみで記述することを考えます。公称ひずみ(添え字 n)と真ひずみ(添え字 t)の関係は式2の通りです。さらに、引張方向の真ひずみと引張方向に対して垂直方向の真ひずみの関係はポアソン比を使って、式3のようにあらわされます。式2と式3から式4が得られ、変形途中の断面積である式1は式5のように書き換えられます。
真応力は変形途中における荷重と断面積の比ですので、式5と引張荷重の比から、真応力は式6のようにあらわされます。
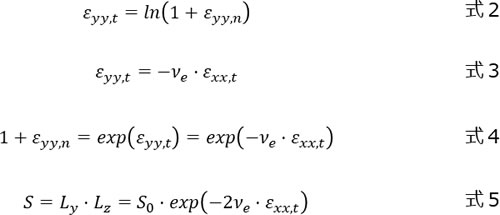
![]()
教科書に書かれている式と異なる?
教科書に掲載されている真応力は恐らく、式7かと思います。式6ではないはずです。では、式6は間違いなのでしょうか?
![]()
いえ、そうではありません。ポアソン比を0.5として式6を見ると式7と一致します。ポアソン比0.5の時は変形に対して体積一定となりますので、式7は金属が塑性状態にあり、体積一定の非圧縮状態で塑性変形が進んでいるときに導出された真応力の式です。
次回は塑性変形を伴うときの真応力を考えます。
関連ページ/参考文献
竹越、丹羽、” MAT_SAMP-1樹脂材料データ作成技術の紹介”、LS-DYNA & JSTAMP Forum 2013 JSOL.
竹越、”塑性体積膨張を示す樹脂の材料データ作成手法の検討”、第57回日本学術会議材料工学連合講演会 日本材料学会 .
●Mat. Curve Modeller:遅れて来たもう一つの材料データ作成ツール – 6
●Mat. Curve Modeller:遅れて来たもう一つの材料データ作成ツール – 4
●Mat.Curve Modellerのページ