樹脂成形とレオロジー 第22回 「樹脂の弾性成分と粘性成分の測定」

動的粘弾性測定装置
これまでに述べてきたように、樹脂は弾性と粘性の両方の成分を所有しており、ここではこの特性の測定法について説明します。
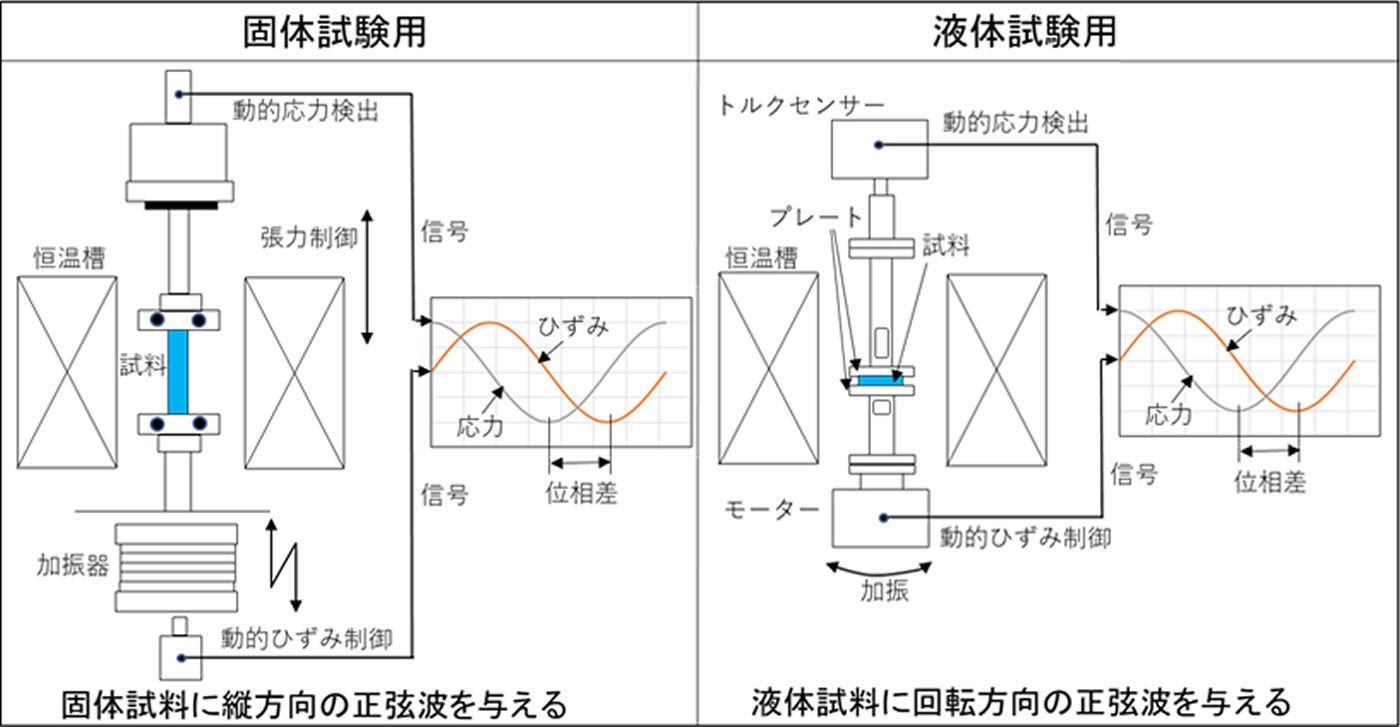
図1に動的粘弾性装置(DMA: Dynamic Mechanical Analyzer)の概略を示します。これは試験片に定常的な正弦波ひずみを与え応答応力を測定し、両者の位相差から粘弾性体の挙動(弾性と粘性成分の寄与、温度特性、周波数特性など)を調べる装置です。図1の左側が固体試験用で、試料の両端を固定し縦方向に正弦波を与えます。試料が液体の場合はこのような形の測定ができませんので、右側のように試料を容器に入れて回転方向の正弦波を与えます。なお、固体試験モードで得られるモジュラス(応力とひずみの関係の係数)は縦弾性率、液体試験モードでは横(せん断)弾性率になります。両者の関係式は第4回「弾性と粘性」で紹介していますので、ご参照ください。樹脂の成形プロセスでは溶融状態を含みますので、右側の液体試験用の測定が一般的です。

純弾性体と純粘性体の挙動
ここでは与えるひずみを \(\varepsilon\) 、発生する応力を \(\sigma\) 、モジュラス(弾性率)をG、粘度を \(\eta\) で表すことにします。
(1) 純弾性体の場合
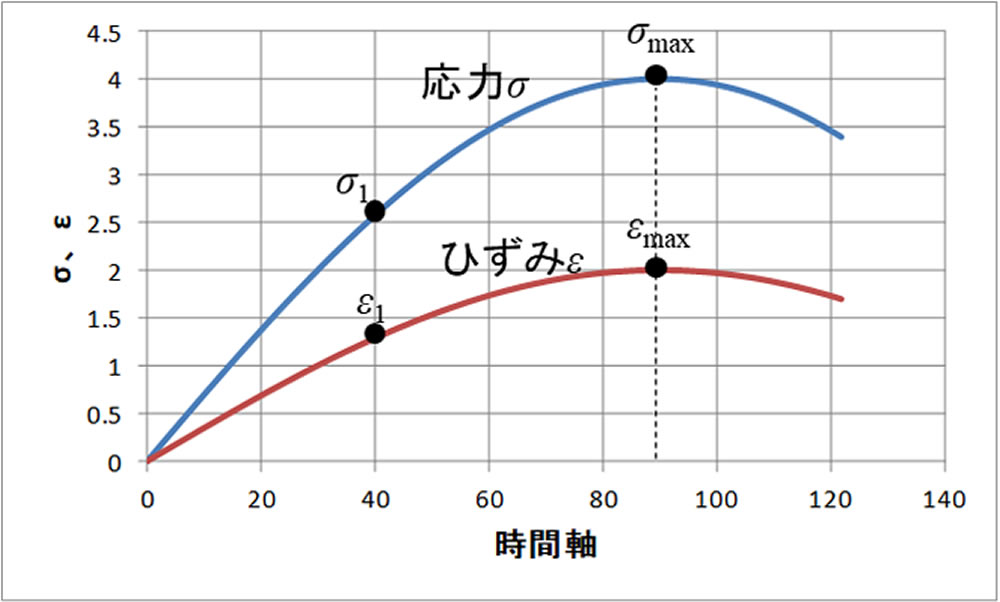
図2に準弾性体の応答特性を示します。横軸は時間になりますが、後述するようにひずみと応力の位相差が重要な特性になりますので、ここでは横軸は360°を1周期としたときの角度の値(°)で表示しています。試料に金属のような純弾性体を用いた場合、発生応力は加えた正弦ひずみにすぐに追随し、位相差は生じません。したがって、どの時刻でも応力 \(\sigma\) とひずみ \(\varepsilon\) の比は一定になります。この比例定数が弾性率Gとなります。
![]()
![]()
(2) 純粘性体の場合
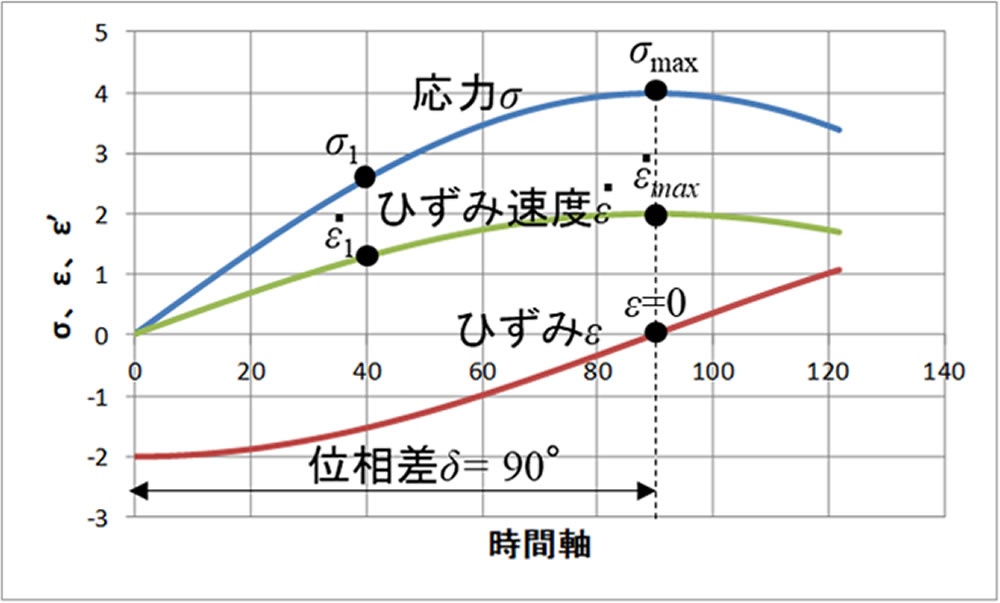
図3に純粘性体の応答特性を示します。弾性の性質を持たない純粘性体では応力はひずみ速度 \(\dot{ \varepsilon\ }\) に比例します。ひずみ速度はひずみの時間変化率であり、正弦波のひずみを与えたとき、ひずみ速度 \(\dot{ \varepsilon\ }\) が最大になるのは図に示したようにひずみが0の箇所になります。ここで最大応力 \(\sigma_{max}\) が生じます。このときのひずみと応力の位相差 \(\delta\) は90°( \(\pi\) /2 )になります。応力 \(\sigma\) とひずみ速度 \(\dot{ \varepsilon\ }\) の比はどの時刻でも一定となり、この比例定数が粘度 \(\eta\) となります。
![]()
![]()
(3) 粘弾性体の場合
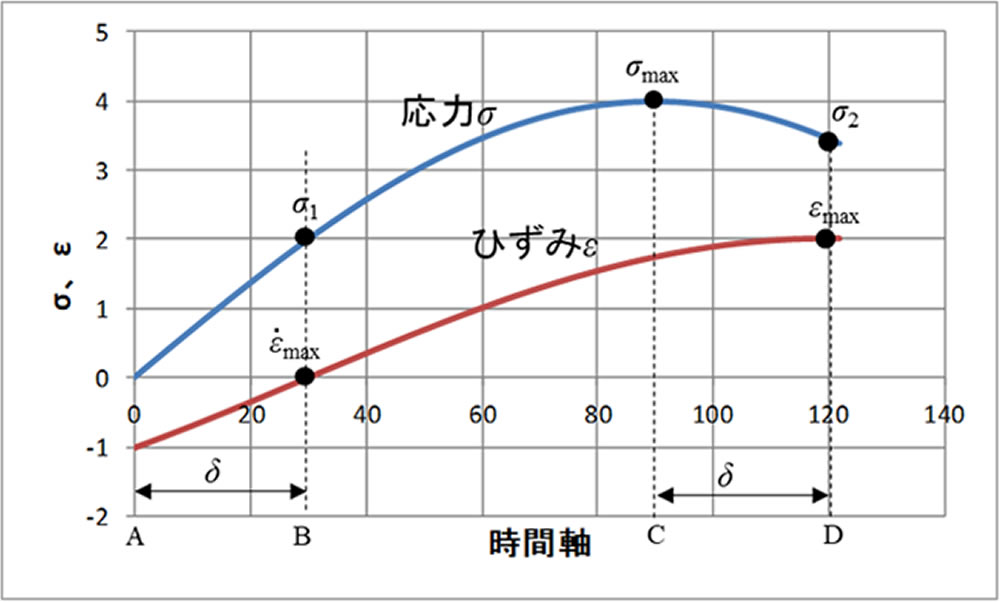
図4に粘弾性体の応答特性を示します。粘弾性体は純弾性体と純粘性体の中間の性質を有し、位相差 \(\delta\) は次の範囲にあります。
粘弾性体 : 0 < \(\delta\) < 90°( \(\pi\) /2 )
粘弾性体ではひずみの最大値 \(\varepsilon_{max}\) が生じたところ(横軸のDの位置)から \(\delta\) だけ遅れて応力の最大値 \(\sigma_{max}\) が発生します(横軸のCの位置)。\(\sigma_{max}\) と \(\varepsilon_{max}\) を用いて(1)式で計算される弾性率を複素弾性率G*(ジースター)とよびます。
![]()
Dの位置はひずみが最大でひずみ速度 \(\dot{ \varepsilon\ }\) は0となります。このことは粘性の寄与が消失している、すなわち弾性成分のみにより応力が発生している箇所を示します。このときの応力 \(\sigma_{2}\) とひずみ \( \varepsilon_{max}\) を用いて計算される弾性率を貯蔵弾性率G’(ジープライム)とよび(4)式で計算できます。さらに(5)式の関係と(3)式を用いると(4)式は(6)式の形になります。
![]()
![]()
![]()
一方、BはDから90°戻った位置で、ひずみが0でひずみ速度 \(\dot{ \varepsilon\ }\) が最大になります。このことは弾性の寄与が消失している、すなわち、粘性成分のみにより応力が発生している箇所を示します。このときの応力 \(\sigma_{1}\) とひずみ速度 \(\dot{ \varepsilon\ }_{max}\) を用いて粘度 \(\eta\) が計算できます。
![]()
![]()
また、ひずみ速度は正弦波ひずみを時間軸方向に1階微分したものであり、正弦波の角周波数を \(\omega\) とすると次の関係があります。
![]()
したがって次式が得られます。
![]()
貯蔵弾性率との対比上、G*sin \(\delta\) は損失弾性率G”(ジーダブルプライム)と定義されます。
![]()
よって、(9)式は次式となります。
![]()
G”とG’の比はtan \(\delta\) となり、これを損失正接といい、タンデルタという言い方のほうが一般的になっています。
![]()
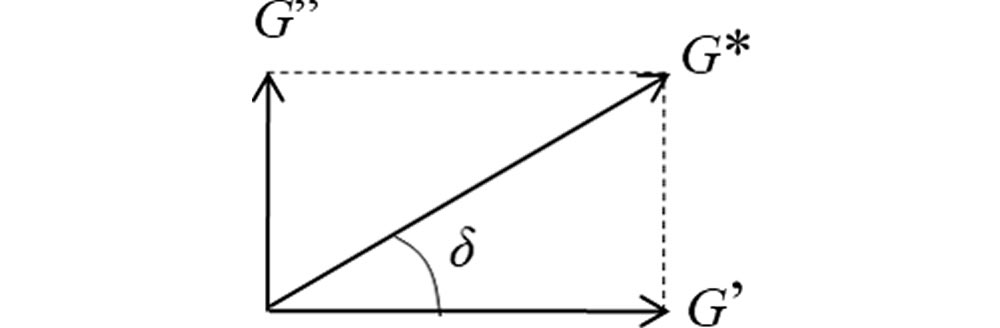
G*、G’、G”と \(\delta\) の関係をわかりやすく書くと図5のようになります。
![]()
また、これから次の関係が得られます。
![]()
G*を \(\omega\) で除した値は粘度の単位になり、これを複素粘度 \(\eta^{+}\) とよび、次式で表されます。
![]()
(9)式、(11)式の \(\eta\) は粘弾性体の粘性部分のみを用いたときの粘度に対し、(14)式の \(\eta^{+}\) は弾性の寄与を含んだ状態での粘度となります。
以上をまとめると下枠内のようになります。位相差 \(\delta\) が小さければ弾性の寄与が大きく、 \(\delta\) の増加とともに粘性の寄与が大きくなっていきます。動的粘弾性装置により、まず、このような特性値が得られます。

次回は周波数を変えたときの特性とそれを基にして得られるCAE解析用のパラメータとの関連についてご説明します。
関連記事/関連ページ
●樹脂成形とレオロジー 第21回 「K-BKZモデルでの伸長粘度の計算例」
●樹脂成形とレオロジー 第23回「樹脂の周波数依存特性からわかること」
