樹脂成形とレオロジー 第23回「樹脂の周波数依存特性からわかること」
前回は動的粘弾性装置において一定周波数で正弦波を与えたときの特性について説明しました。今回はそれに引き続き、特性値の周波数依存性と、その特性値の活用法について述べます。
貯蔵弾性率と損失弾性率の変化
これまでに述べてきたように、樹脂は弾性と粘性の両方の成分を所有しており、ここではこの特性の測定法について説明します。
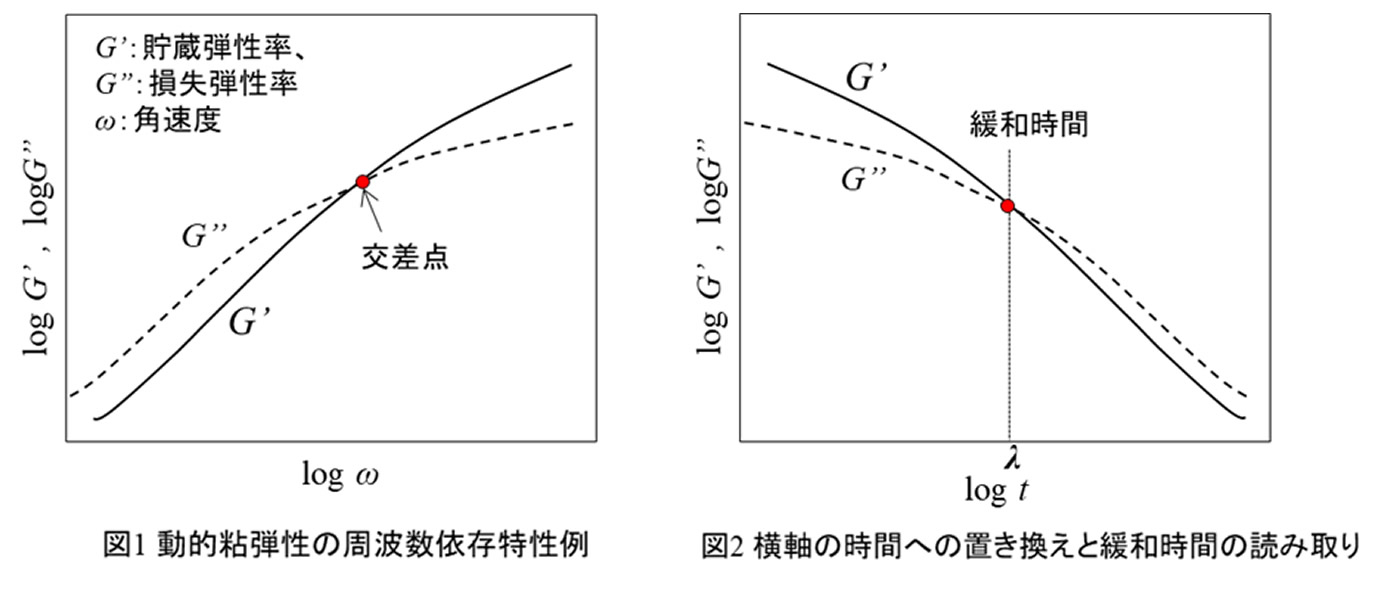
図1に動的粘弾性装置で周波数を変えたときの特性例を示します。角周波数 \(\omega\) の増加とともに弾性の寄与を示す貯蔵弾性率G’、粘性の寄与を表す損失弾性率G’’とも増加します。広範囲の \(\omega\) を用いると、 \(\omega\) が小さいときにはG’’ > G’になり、所定の \(\omega\) でG’’ = G’となる交差点(Crossover point) が存在します。これより大きい \(\omega\) ではG’ > G’’ となります。ここで横軸を時間に直します。ここでは時間tは次式で求めることにします。
![]()
時間tを用いると図2が得られます。G’とG’’が同じ値を示すときが、弾性と粘性の寄与が等しくなった状態を示し、粘弾性体の理論の定義からこの時刻が緩和時間 \(\lambda\) となります。実際には測定ばらつきによりG’’ = G’となる交差点が見つけにくいこと、実験範囲の外に交差点がある場合もあり、以下に述べる理論的な取り扱いから \(\lambda\) を特定するとともに緩和弾性率曲線に直す方法を用いることが一般的です。
二要素Maxwellモデルでの周波数依存特性
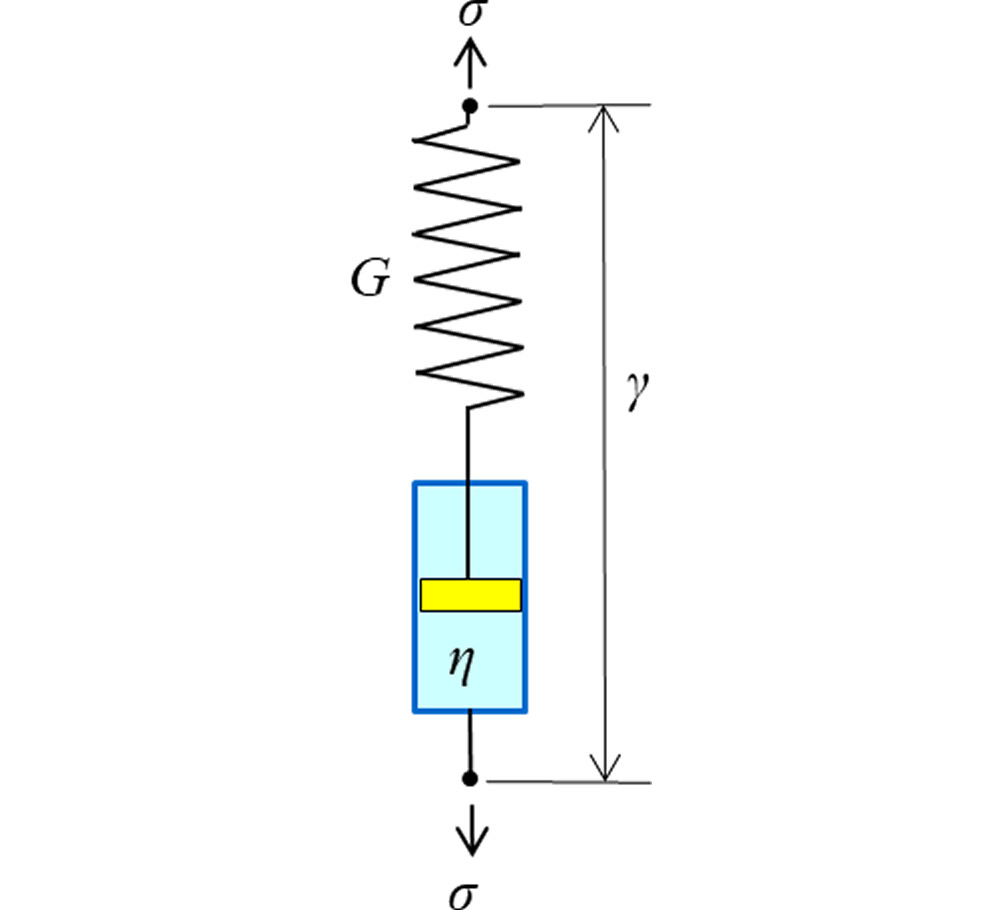
ここでは、CAEで緩和弾性率特性を表すときに用いるばね、ダッシュポットモデルの係数の値と周波数依存特性の関連を調べます。まず、最初に現象を単純化するために図3に示す二要素Maxwellモデルを用いることにします。
![]()
このモデルの運動方程式は次式となります。これは第5回「粘弾性体のモデル化」の(4)式に示したものと同じです。
![]()
![]()
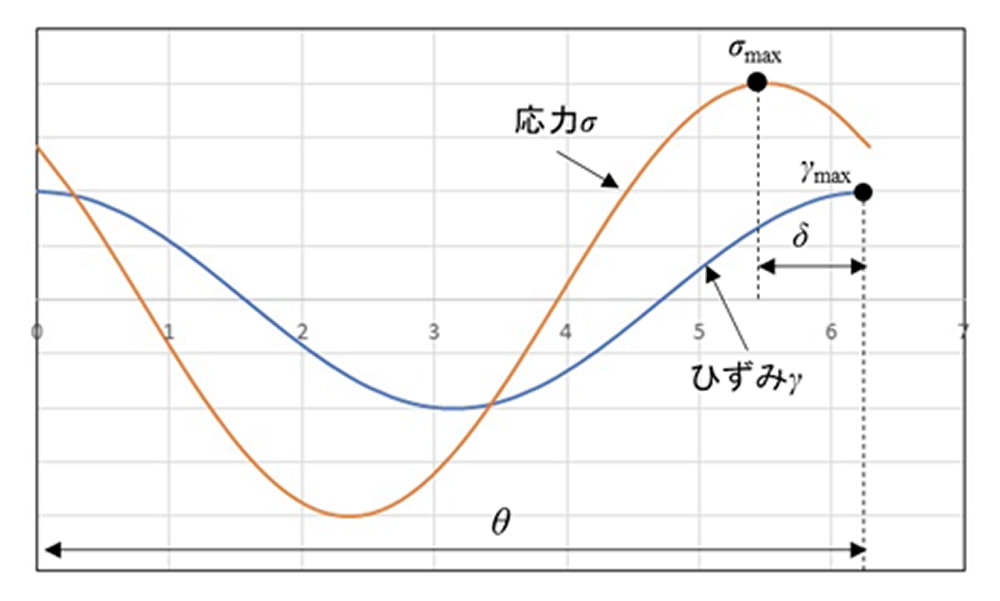
ここで、 \(\sigma\) :応力、t:時間、 \(\lambda\) :緩和時間、 \(\gamma\) :ひずみ、G:ばね要素弾性率、 \(\eta\) :ダッシュポット要素粘度です。(2)式の左辺は時刻tにおける応力の変化率にそのときの応力を \(\lambda\) で除した値の足し合わせになり、右辺はその時刻でのひずみの変化率(ひずみ速度)にGを掛けた値となります。応力とひずみがどう対応するかを表しています。一方、動的粘弾性装置で角周波数 \(\omega\) を与えて得られる特性は図4のようになります。ここではひずみ発生後ちょうど1周期過ぎた状態を示しています。
![]()
応力はひずみよりも \(\delta\) だけ遅れた波形になりますので、ひずみが角度 \(\theta\) 進んだところでの応力は次式となります。
![]()
ここで \(\sigma_{max}\) は発生応力の最大値です。 \(\theta\) の代わりに角周波数 \(\omega\) を用いると次式になります。
![]()
加法定理を用いると次式になります。
![]()
一方、前回ご紹介しましたように次式の関係があります。
![]()
![]()
ここで、 G* :複素弾性率、 G’:貯蔵弾性率、 G”:損失弾性率です。また、 G*は次式で得られます。
![]()
\(\gamma_{max}\) :ひずみの最大値です。
(7)~(9)式の関係を用いると(6)式は次式となります。
![]()
ここで重要なことは、Gと \(\lambda\) を定数とする(2)式に、動的粘弾性装置で得られるG’とG”の周波数依存特性値が入ってきたことです。これはG’とG” という実験データを基にして、応力解析で使用するパラメータであるGと \(\lambda\) を特定できることを示唆しています。しかし、 (2)式の形のままで解を求めるのは容易ではなく、この場合は複素数を利用して解を求める方法が用いられています1)。その結果を次に示します。
![]()
![]()
![]()
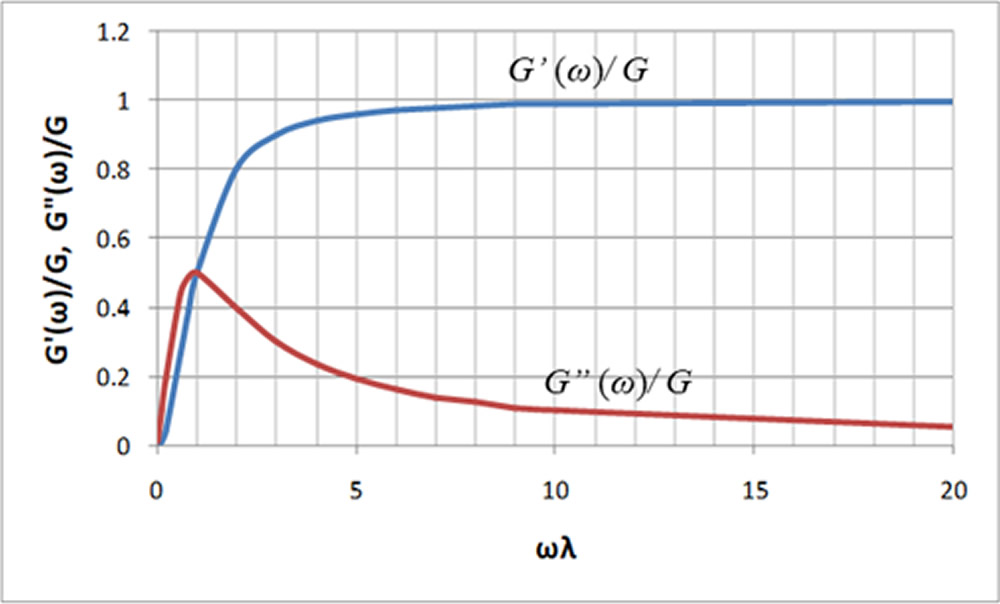
(11)式は複素数の形ですが、(12)式、(13)式は実数の形になっています。いずれも左辺は動的粘弾性試験で求められる周波数依存特性です。右辺は緩和弾性率を表現するのに必要な定数であるGと \(\lambda\) 、ならびに左辺の値が求められたときの角周波数 \(\omega\) が入っています。今、横軸を\(\omega\)\(\lambda\) にして、縦軸をG’/G, G”/Gで無次元化したときの特性値を図 5に示します。\(\omega\)\(\lambda\)<1のときにG”>G’となり、\(\omega\)\(\lambda\)=1( \(\omega\) =1/ \(\lambda\) )でG”=G’=G/2となります。ここが図1で示した交差点になり、\(\omega\)を与えれば緩和時間λが求められます。 \(\omega\) \(\lambda\) >1ではG”は値が小さくなり、 G’は増加を続けます。\(\omega\)\(\lambda\) =10( \(\omega\) =10/ \(\lambda\) )程度でG’はGの値に飽和します。すなわち、図3の二要素MaxwellモデルでのGと \(\lambda\) が求められます。二要素Maxwellモデルでは必ずこの特性を示しますが、実材料ではこの形になりません。したがって、次に示す一般化Maxwellモデルを用いて実材料に合うようにパラメータを増やす操作が行われます。
![]()
実材料の緩和弾性率特性の作成
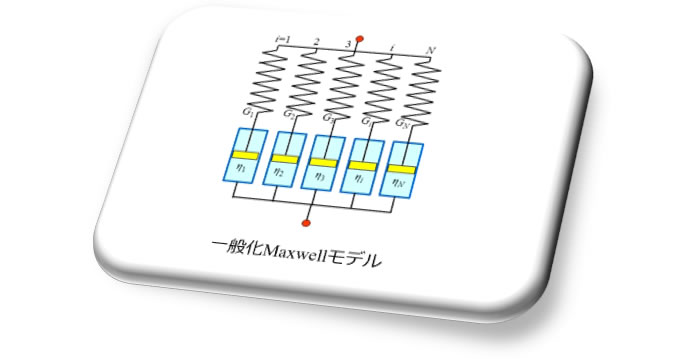
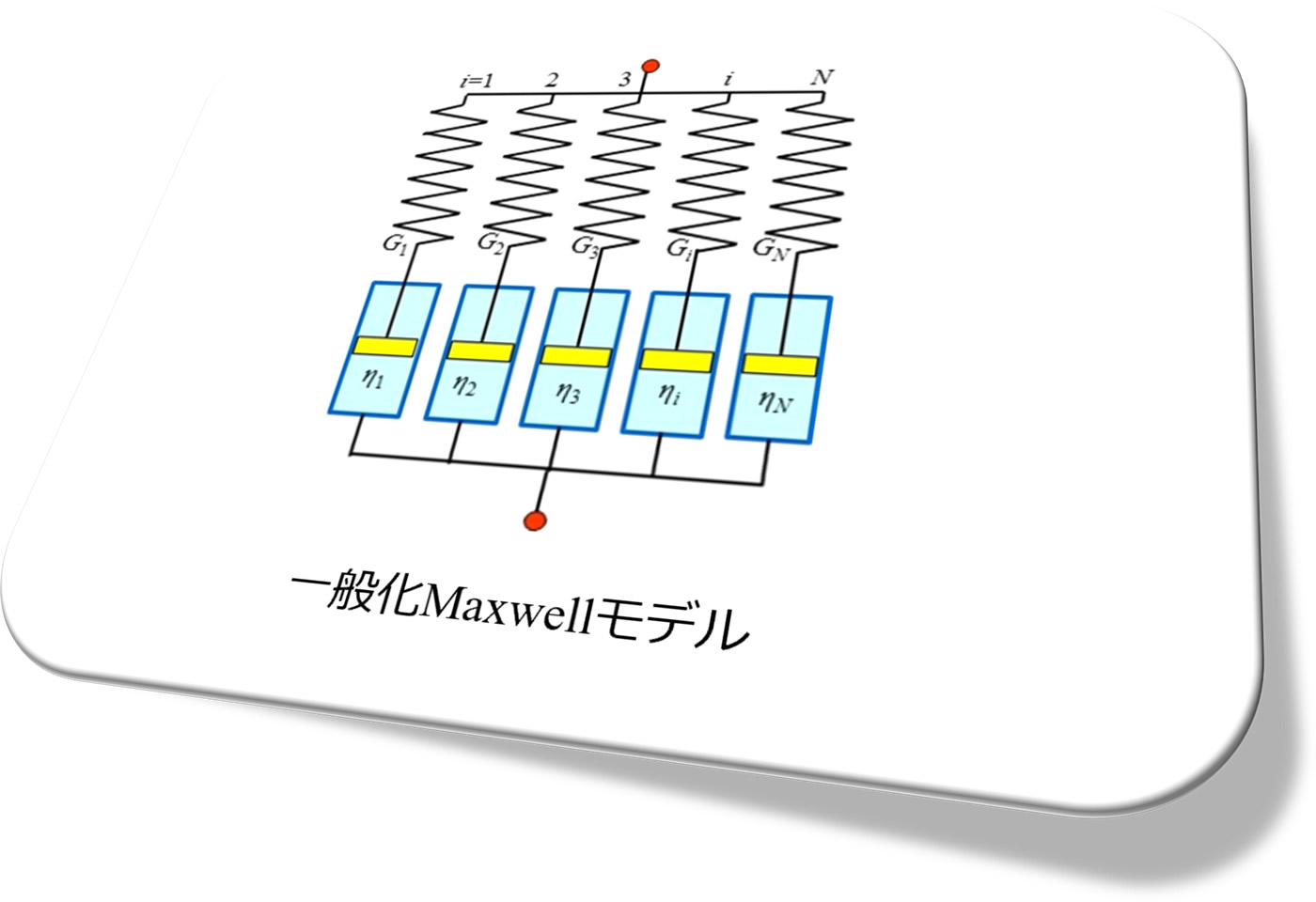
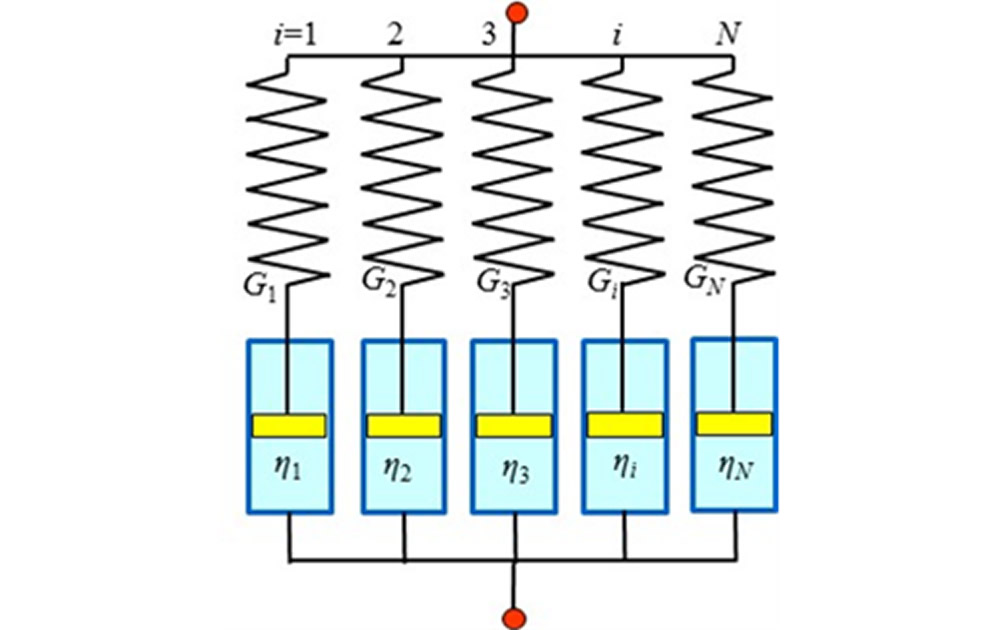
実材料の応力緩和特性を表すとき、通常図6に示す一般化Maxwellモデルを用います。
![]()
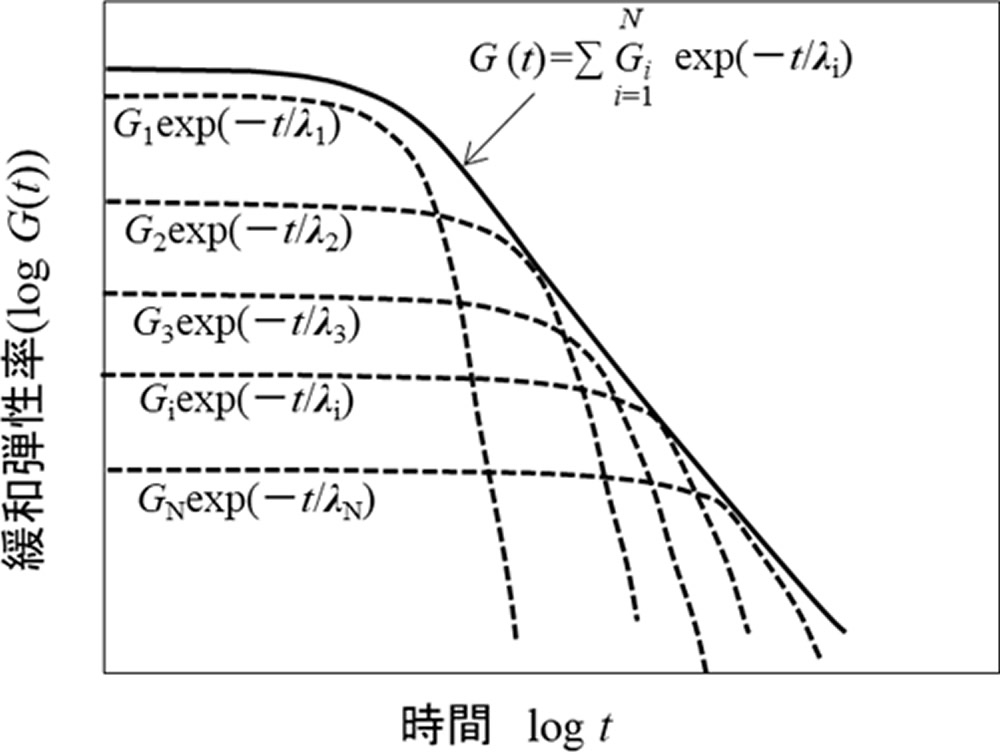
緩和弾性率は次式で計算されます。
![]()
![]()
一方、動的粘弾性装置での実験により得られるG’、G”とCAE解析で用いる一般化Maxwellモデル中の係数(緩和スペクトル)の関係は次式となります。最適化手法を用いてGi , \(\lambda_{i}\) が決定できます。
![]()
![]()
このようにして求めたGi , \(\lambda_{i}\) を用いて図6のように緩和弾性率曲線が得られます。Gi , \(\lambda_{i}\) の値は樹脂の粘弾性を考慮した応力、流動解析に使われています。
![]()
参考URL:1) ●http://ctwww.yz.yamagata-u.ac.jp/takimoto/rheo/pdf/Maxwell.pdf
関連記事/関連ページ
●樹脂成形とレオロジー 第22回 「樹脂の弾性成分と粘性成分の測定」
●樹脂成形とレオロジー 第24回「樹脂の周波数依存特性の一般化Maxwellモデルへの変換」