樹脂成形とレオロジー第25回「複素粘度の利用法」 │ DISCOVER CAE

樹脂成形とレオロジー第25回「複素粘度の利用法」

動的粘弾性装置での周波数依存特性の一つに複素粘度があります。ここでは、その利用法について説明します。

複素粘度の特性

複素粘度は次式で示されます。

緩和弾性率の表現方法は弾性体に粘性の寄与を考慮した構造解析の分野と、粘性体に弾性の寄与を考慮した樹脂流動解析の分野で異なっており、その違いを説明します。

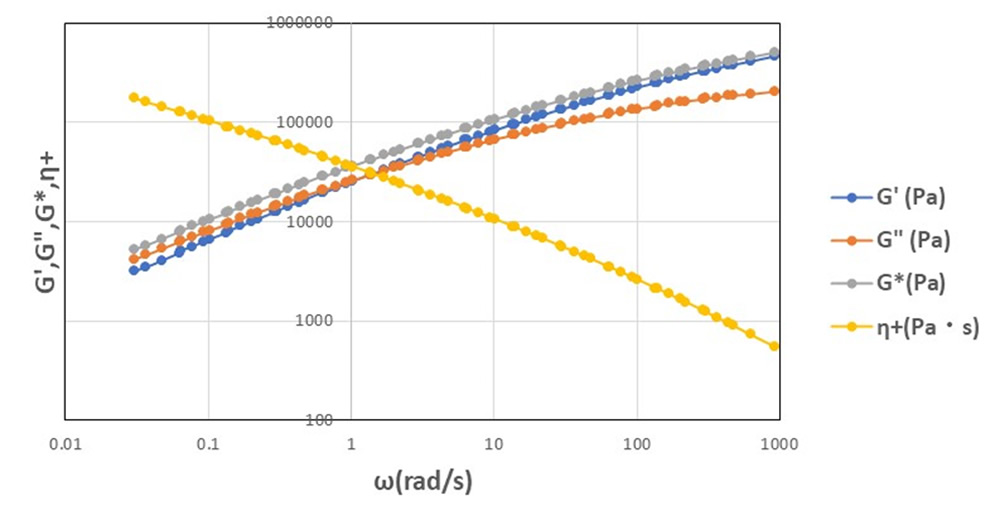
ここで、 \(\eta\)⁺：複素粘度、 G^*：複素弾性率、G’：貯蔵弾性率、G”：損失弾性率、\(\omega\)：角周波数です。ここでも前回用いた樹脂Aの特性を用いることにします。図1にG’、 G’’、 G^*の周波数依存特性ならびに(1)式で計算した \(\eta\)⁺の特性を併せて示します。この \(\omega\) の範囲内ではωの増加とともにG’ 、G’’、 G^*の値は増加しますが、 \(\eta\)⁺は G^* を \(\omega\) で割るので \(\omega\) の増加とともに値が低下する特性を示します。

コックスメルツ則(The Cox-Merz rule)について

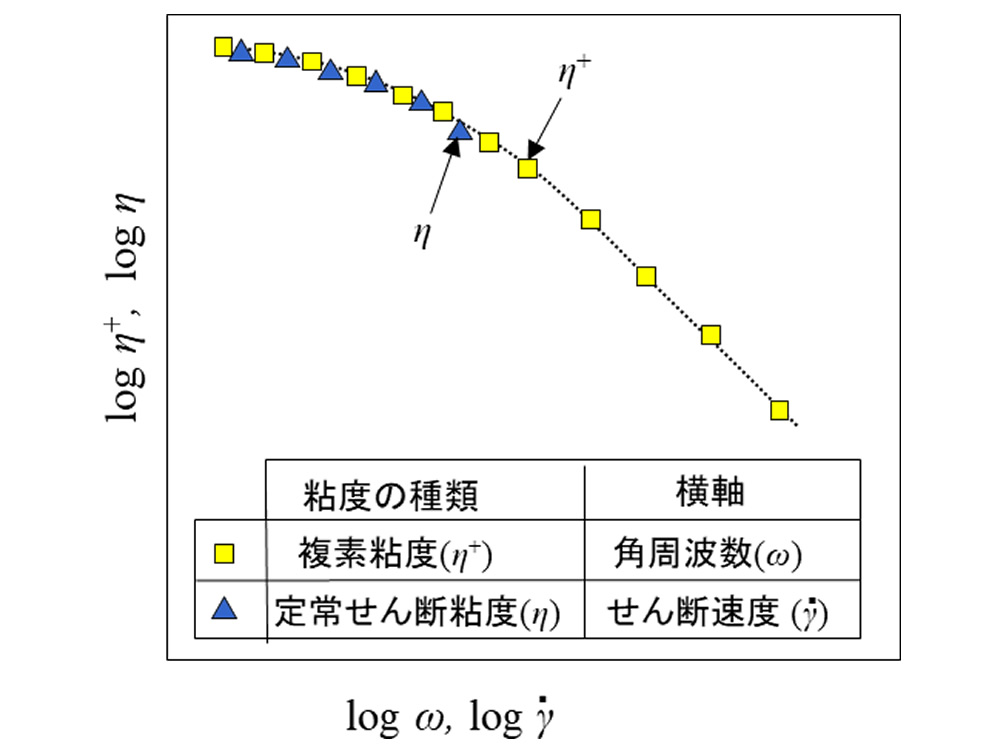
動的粘弾性装置で用いる角周波数 \(\omega\) と定常せん断粘度計で得られるせん断速度 \(\dot{\gamma\ }\) は時間の逆数という同じ単位になります。ここで、横軸を \(\omega\) ならびに \(\dot{\gamma\ }\) とし、複素粘度 \(\eta\)⁺ と定常せん断粘度 \(\eta\) を縦軸にしたときに、図2のように \(\eta\)⁺と \(\eta\) が重なった状態になったとします。このとき、動的粘弾性装置で用いた角速度 \(\omega\) は定常せん断流動実験で用いたせん断速度 \(\dot{\gamma\ }\) と等価とみなすことができます。図2の状態が得られるときにコックスメルツ則(The Cox-Merz rule)という経験則が成り立つとされています。この場合、粘度のせん断速度依存性はCross モデルなどに当てはめてその係数を求めることができます。

コックスメルツ則が成立と仮定したときの粘度式の作成

ここでは図1の横軸をせん断速度に、複素粘度をせん断粘度に置き換えてみます。また、Crossモデルへ当てはめて係数を求めてみます。Crossモデルは次式となります。

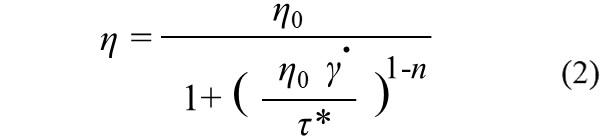
ここで、 \(\eta\) ：せん断粘度、 \(\dot{\gamma\ }\) ：せん断速度、 \(\eta\)₀ ：ゼロシェア粘度、 n ：構造粘度指数、 \(\tau\)^*：係数です。このモデルは第17回「熱硬化性樹脂の粘度式」のところでご紹介しましたが、せん断速度の小さいところで値が飽和し、せん断速度の増加とともに粘度が低下してくる特性があり図1の \(\eta\)⁺ のような形のモデル化に適していると考えられます。ここでも、なめらかな非線形関数での最適解を求めるのに適したGRG(Generalized Reduced Gradient)非線形ソルバー¹⁾を用い、係数を最適化してみました。結果を表1に示します。

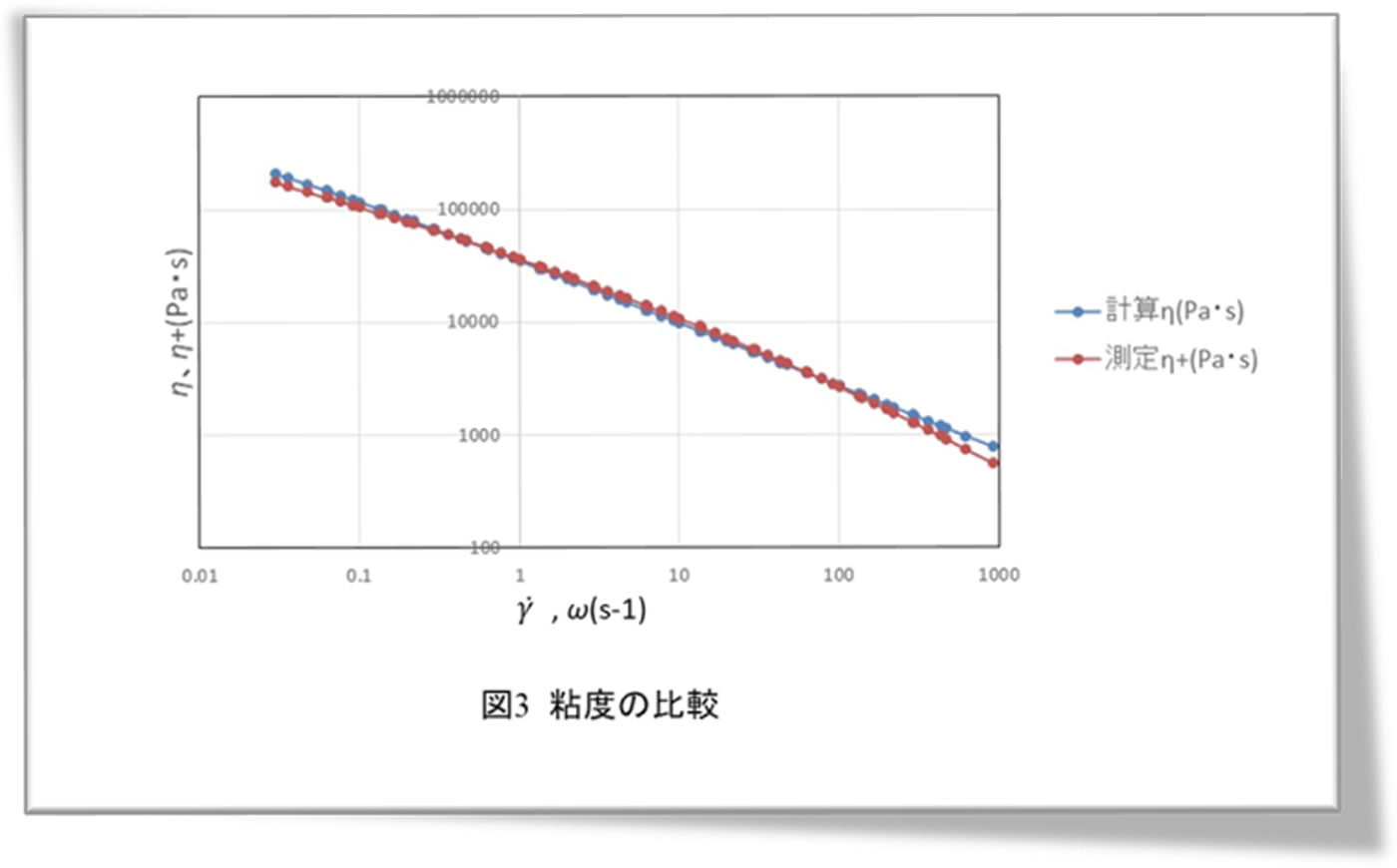
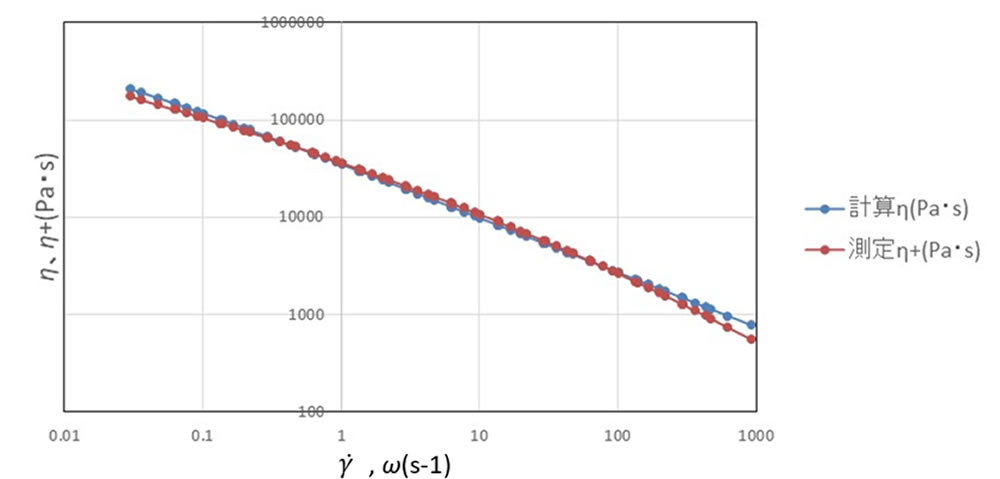
粘度の比較結果を図3に示します。表1の係数を用いてCrossモデルで計算されたせん断粘度 \(\eta\) は測定から得られた複素粘度 \(\eta\)⁺ と比較的よく一致していることがわかりました。せん断粘度は専用の回転粘度計を用いて測定するのが理想ですが、用いる樹脂の粘性が高すぎて測定しにくい場合などには、動的粘弾性装置での周波数特性から複素粘度を求め、これに各種粘度モデル式をあてはめるという方法も用いることができます。

参考URL:1）https://ja.helpr.me/9661-what-is-grg-nonlinear-solver