樹脂成形とレオロジー第28回「流路断面形状の抵抗値について」
樹脂が管内を流れるときの圧力損失は流量、樹脂粘度、流動距離、断面の代表長さとその形状によって決まります。ここでは断面形状に注目し、その抵抗値の評価法について述べます。
水力平均深さm 値による評価法
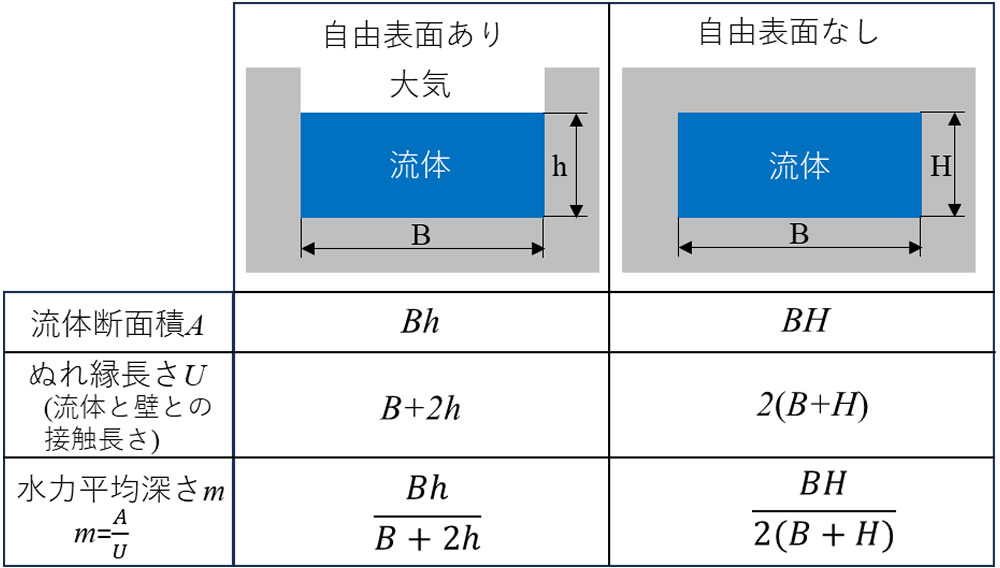
流体は通常壁に付着しますので、同じ断面積なら付着部分が長い断面形状の方が流動抵抗が大きくなります。これを表す指標が水力平均深さm 値であり次式となります1)。
\begin{align*}m &= \frac{A}{U} &\qquad ・・・・・・・(1)\end{align*}
ここで、A :流体の断面積、U :ぬれ縁長さ(流体と壁との接触長さ)です。m 値が小さいほど流れにくくなります。図1に矩形断面流路でのm 値の計算例を示します。同じ断面積でも自由表面ありとなしでU の値が異なりm も違った値になります。樹脂成形では通常樹脂は自由表面なしの状態で流動しますので、以後の解析はその状態になっていることを前提とします。
![]()
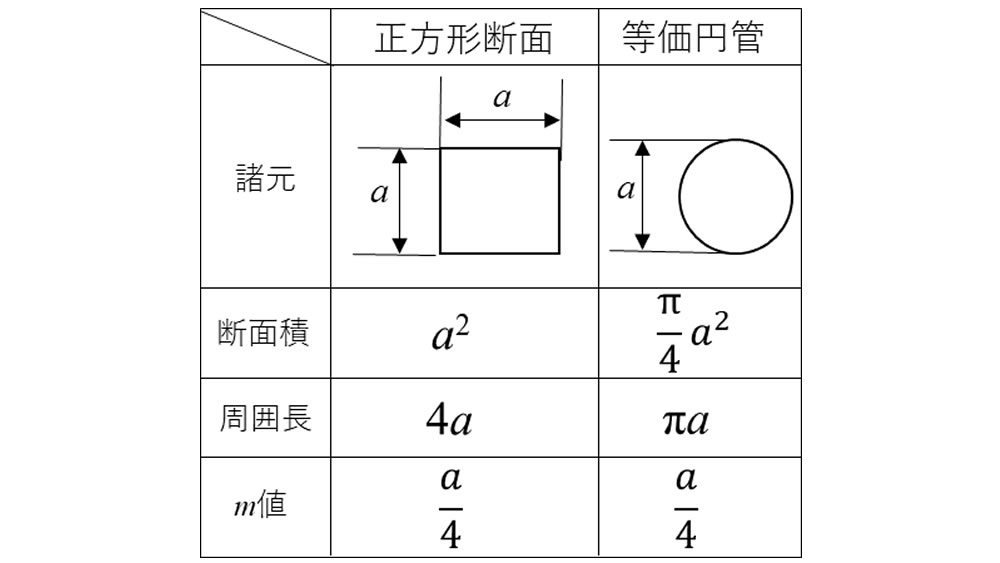
樹脂成形のように管内を液体が満たして流れる場合はぬれ縁長さは断面の周囲長になります。円管で計算すると半径の半分がm になり、代表長さである直径はその4倍の値になります。円管以外の断面形状の場合、(1)式でm 値を求め、これを4倍した値が等価円管に置き換えたときの直径になります。複雑な断面形状でも流動抵抗が等価な円管に置き換えられるので、その後の計算が楽になるというメリットがあります。
ここで、正方形断面を等価円管に置き換えてみますと図2のようになります。等価円管に置き換えたとき、元の正方形断面よりも断面積が小さくなっています。もし、現実の正方形断面流路を計算の簡素化のためにm 値を揃えた円管に置き換えたとしますと、同じ流量でも流速が異なり、対象流動区間の通過時間が違ってきます。すなわち、実際と計算とで充填完了時間が異なってくるという問題を生じます。一方、m 値は流体力学で乱流領域を対象にして使われてきました1)。樹脂流動のような層流に対しては流動抵抗が等価な形状にはできにくいことも分かっています。
以上から、ここではm 値を使わない抵抗値の評価法について説明していきます。
![]()
運動方程式
まず、運動方程式に戻って検討します。同じ断面形状の流路内をニュートン流体が等温、定常、層流状態で1方向に流動している場合を考えます。図3に矩形断面流路での座標軸と速度の方向を示します。ここでW :流路幅、h :流路深さ、L :流動距離です。速度uはx方向のみに生じ、y方向とz方向に沿って速度分布ができます。
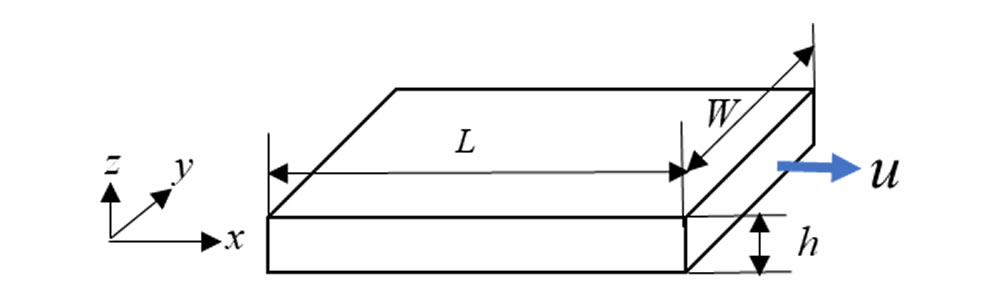
![]()
このときの運動方程式は次式となります。ここで、P :圧力、\(\eta\) :粘度です。この形の式は二次元のポアソン方程式とよばれ、弾性学や電磁気学などで定常状態での各種物理現象を記述する際にも現れます。
\begin{align*}
0=-\frac{\partial P}{\partial x}+\eta(\frac{\partial^{2}u}{\partial y^{2}}+\frac{\partial^{2}u}{\partial z^{2}})\qquad ・・・・・・・(2)
\end{align*}
(2)式を境界条件を用いて解くと図4のような速度分布が得られます2)。これを積分すると流量Q が得られます。これらの厳密解はh とW の値と比をパラメータとする双曲線関数を用いた無限級数の形になります1),2)。しかし、このままでは利用しにくいので、W ≫h のときに得られる平板流の圧力損失の式をベースにして、使いやすい形にしていきます。
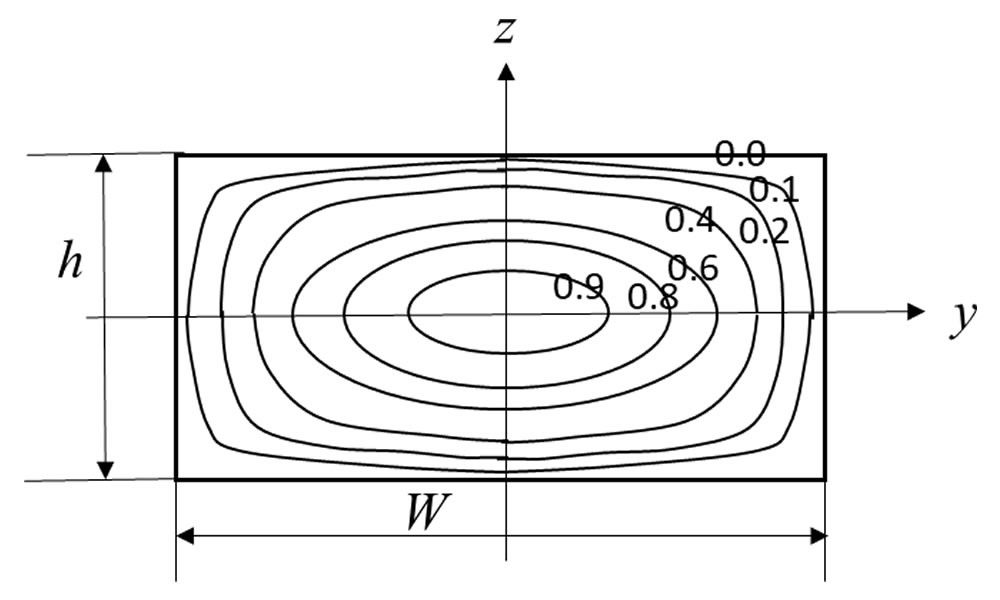

平板流の解
W ≫h のとき、速度分布はz方向のみに生じるとみなせますので、(2)式は次の形になります。
\begin{align*}
0=-\frac{\partial P}{\partial x}+\eta(\frac{\partial^{2}u}{\partial z^{2}})\qquad ・・・・・・・(3)
\end{align*}
これを解くと次式が得られます。
\begin{align*}
\Delta P = \frac{12\eta QL}{Wh^3} \qquad ・・・・・・・(4)
\end{align*}
ここで、\(\Delta\)P :圧力損失、\(\eta\) :粘度、Q :体積流量、L :流動距離、W :流路幅、h :流路深さです。図5に(4)式の粘度以外の記号を用いた略図を示します。
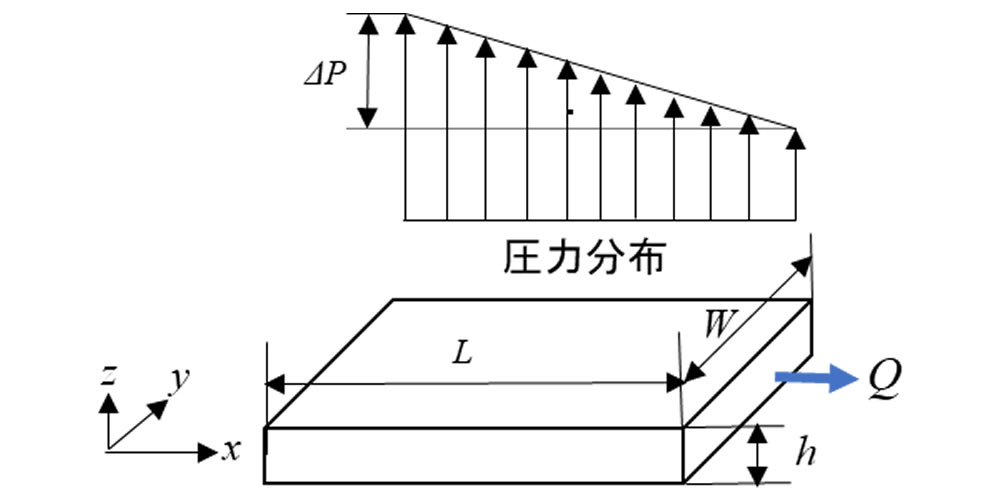
![]()
形状係数F の適用
ここで図4の速度分布の状況に対応させるために形状係数F を右辺の分母に加えます2)。
\begin{align*}
\Delta P = \frac{12\eta QL}{Wh^3 F} \qquad ・・・・・・・(5)
\end{align*}
(2)式の理論解の高次の微少量を無視し、F に該当する箇所を抽出すると次式が得られます2)。
\begin{align*}
F = 1-0.6274(\frac{h}{W}) (tanh\frac{\pi}{2}\frac{W}{h}+0.0045) \qquad ・・・・・・・(6)
\end{align*}
この式はW ≧h でF =1となり、(4)式と一致します。h /W の増加すなわちh がW の値に近づくにしたがってF は小さくなります。そしてW =h のときは正方形断面の流路となり、このときはF =0.4217となり理論解と一致します。一方、(2)式に示した粘性流体の管内の流れの基礎方程式は同じ断面形の棒をねじる際に生じる応力の微分方程式と同一形となりますので、弾性学の公式集に各種断面形状でのF に該当する値が記載されています3)。このときの矩形断面でのF は次式で示されます3)。
\begin{align*}
F = 1-0.63(\frac{h}{W}) (1-\frac{1}{12}(\frac{h}{W})^4) \qquad ・・・・・・・(7)
\end{align*}
値を比較してみると(6)式と(7)式の誤差は最大で0.5%程度なので、どちらを使用しても問題はありません。
各種断面での形状係数F
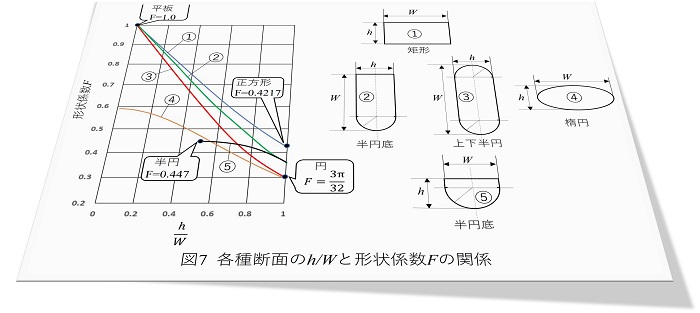
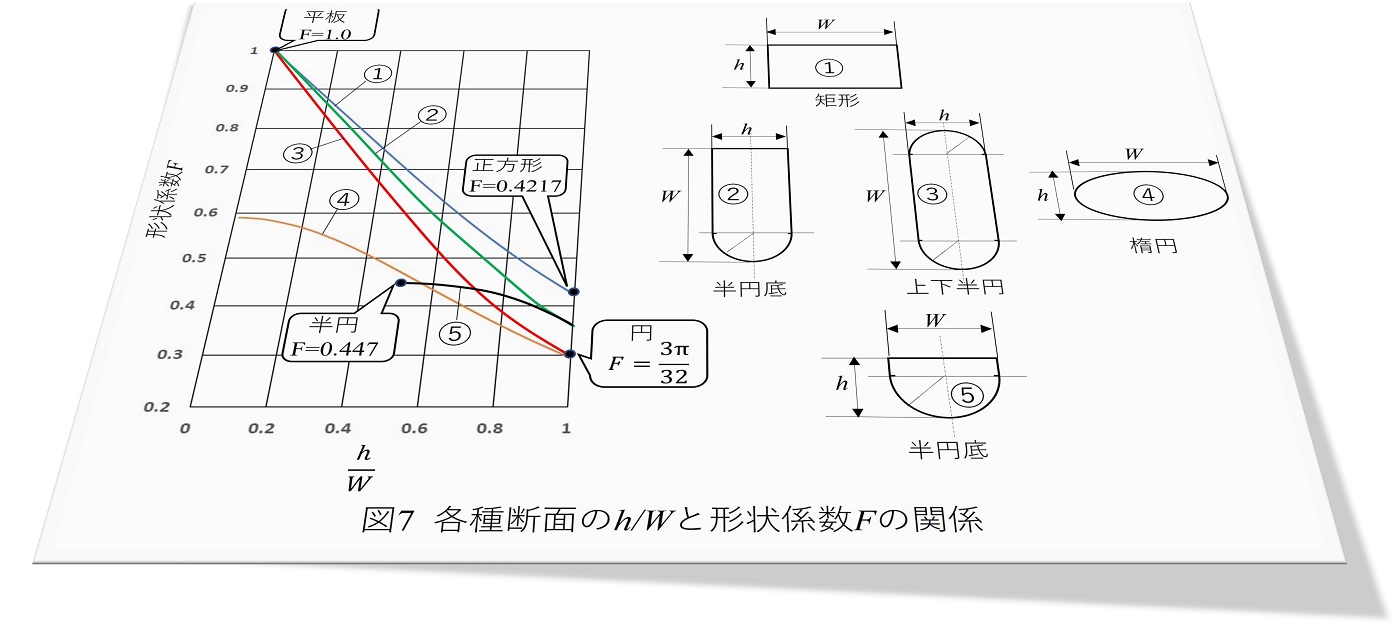
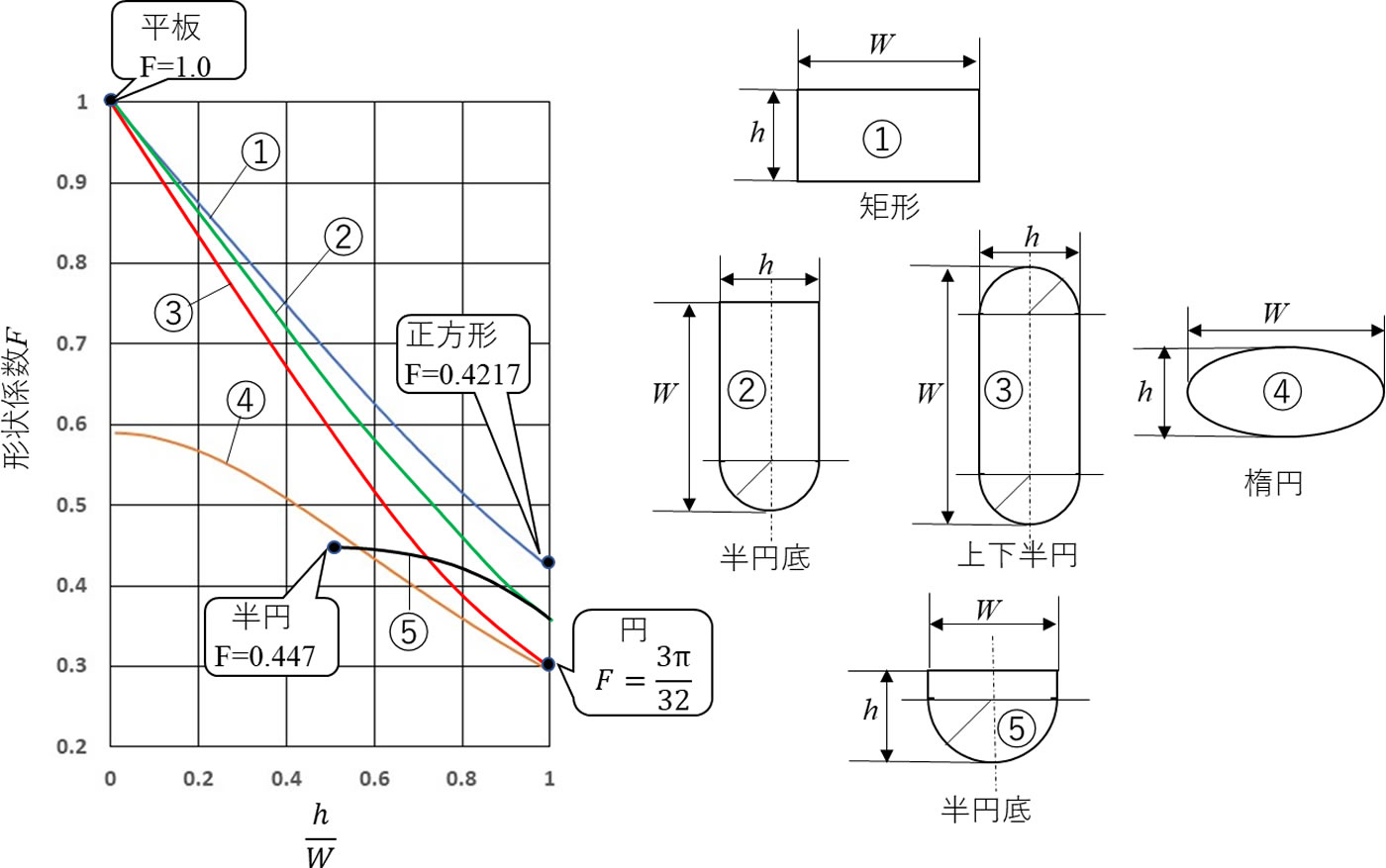
(5)式の前提はW ≧h でした。各種断面に適用する場合、W は断面の長辺、h は断面の短辺という定義になります。図6に各種断面形状と形状係数F を示します。断面が円のときは表中の形状係数F を用いると、円管内の流動式であるポアゼイユの式と一致します。楕円でW =h とするとこれは円になり、円のF と一致します。
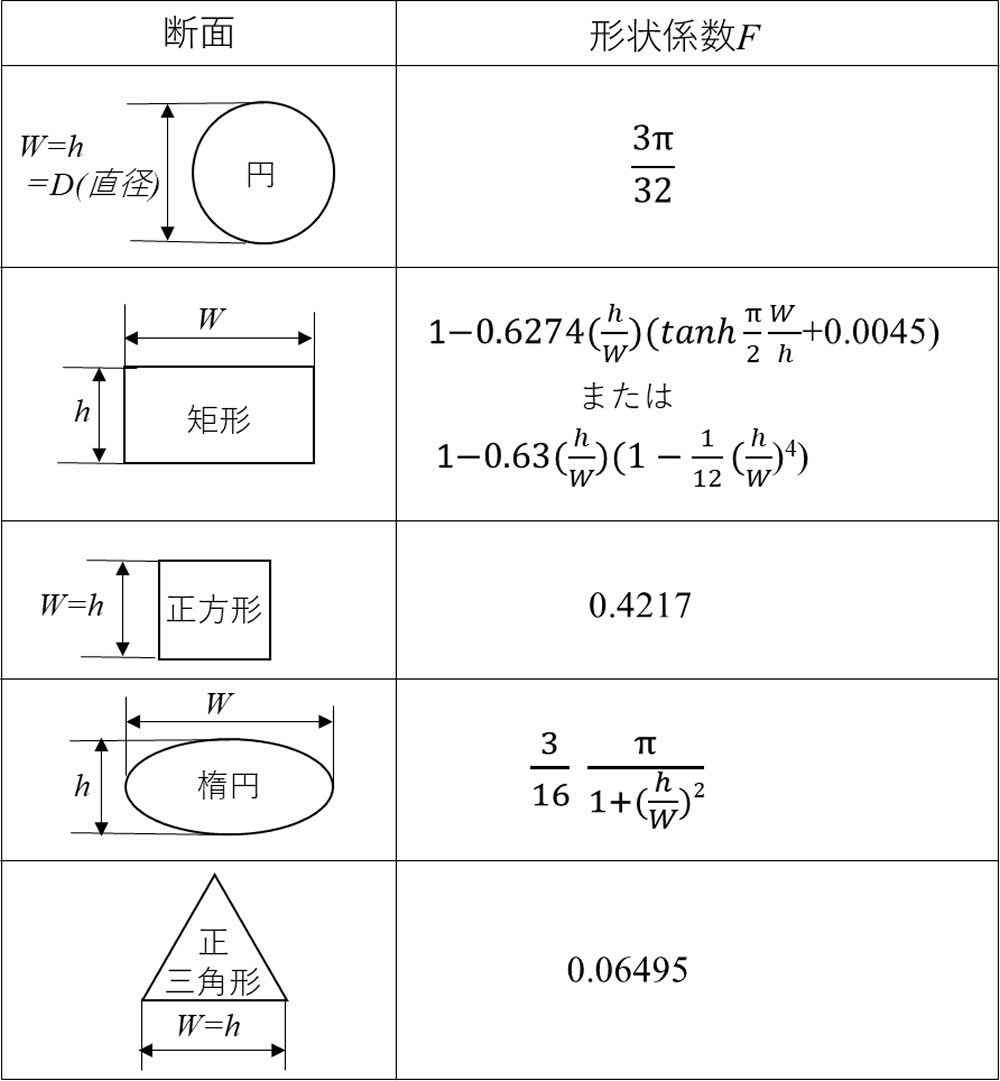
![]()
図7に各種断面のh /W と形状係数Fの関係を示します。②、③、⑤の形状はこれまでにでてきませんでしたが、これはLahtiが数値解析により求めたものです4)。半円底の断面は実際の金型流路でも使われています。ここで述べてきた手法はニュートン流体を前提としていますので、非ニュートン流体である実際の樹脂流動時の圧力、流量の絶対値の予測はできませんが、図6、図7から流路形状起因の抵抗値を加味した上で、プロセス最適化の方向付けに有力なツールになります。
![]()
参考文献
1)板谷松樹:水力学, 朝倉書店(1968)
2)伊藤公正:プラスチック異形押出の技術, 工業調査会(1974)
3)J.R.Roark:Formulas for Stress and Strain, McGRAW HILL KOGAKUSHA (1965)
4)G.P.Lahti:Calculation of Pressure Drops and Outputs, SPE journal(1963)
関連記事/関連ページ