樹脂成形とレオロジー第29回「指数則モデルの実材料への適用例」 │ DISCOVER CAE

樹脂成形とレオロジー第29回「指数則モデルの実材料への適用例」

高分子溶融体は一般的にせん断速度が大きくなると粘度が低下する性質を持ちます。この状況を表すモデル式が色々と提案されています。ここでは、指数則モデルを実材料へ適用した例を示します。

指数則モデルの特性

指数則モデルを(1)式に示します。ここで、 \(\eta\) ：粘度、 \(\kappa\) ：擬塑性粘度、 \(\dot{\gamma\ }\) ：せん断速度、 n ：構造粘度指数です。

\begin{align*}\eta &= \kappa \dot{\gamma}^{n-1} &\qquad ・・・・・・・(1)\end{align*}

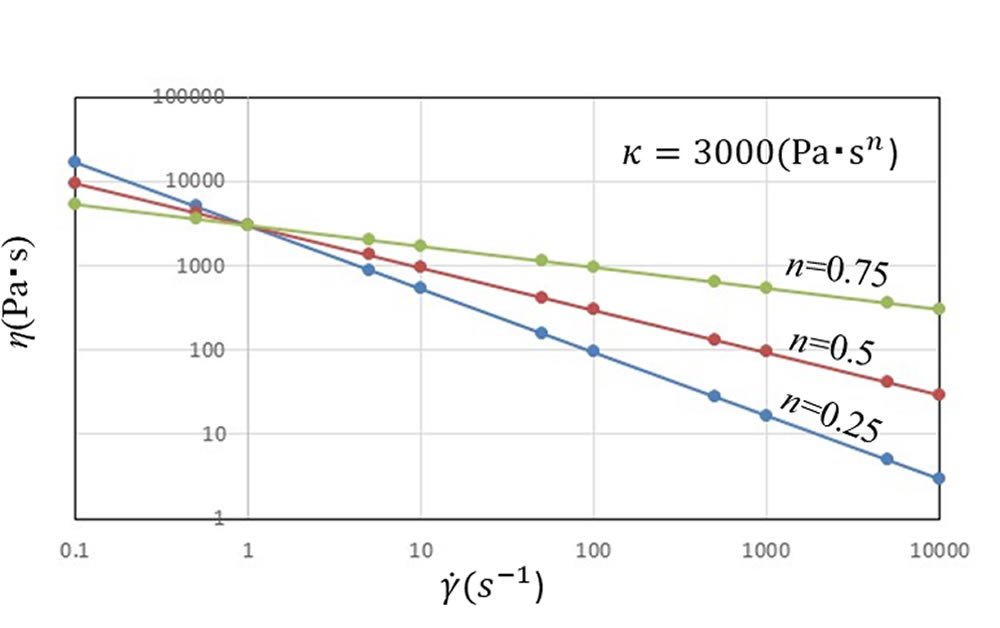
n <1のとき粘度とせん断速度の両対数座標上で右下がりの直線関係が得られます。図1に \(\kappa\) を固定してn を変えたときの特性を示します。n が小さくなるにしたがい負の勾配が大きくなり、 \(\dot{\gamma\ }\) =1s^-1のところでn によらず \(\eta\) が \(\kappa\) の値と一致します。

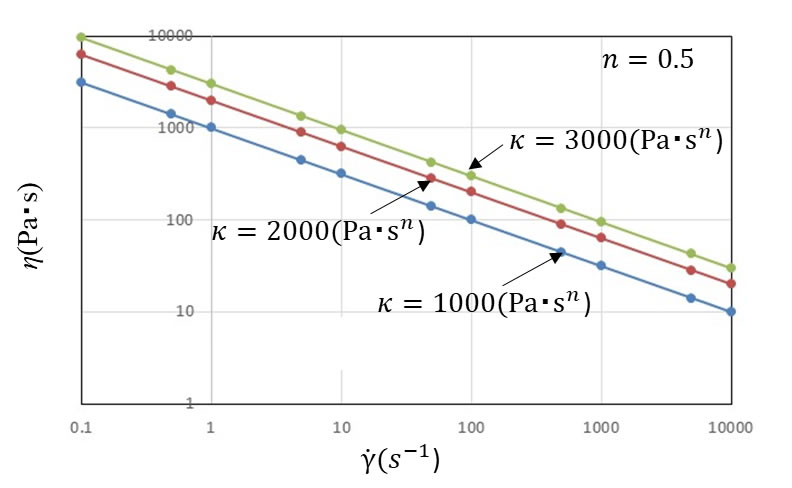
図2にn を固定して \(\kappa\) を変えたときの特性を示します。いずれも勾配は同じで \(\kappa\) が大きいほど粘度が高くなります。粘度とせん断速度の両対数座標上でこのような直線関係に近い特性を示す樹脂は指数則モデルにあてはめることができます。ただし、このモデルは \(\dot{\gamma\ }\) =0で発散しますので、所定のせん断速度以下の領域で飽和する粘度を与えておく必要があります。

温度依存モデルとの組み合わせ方

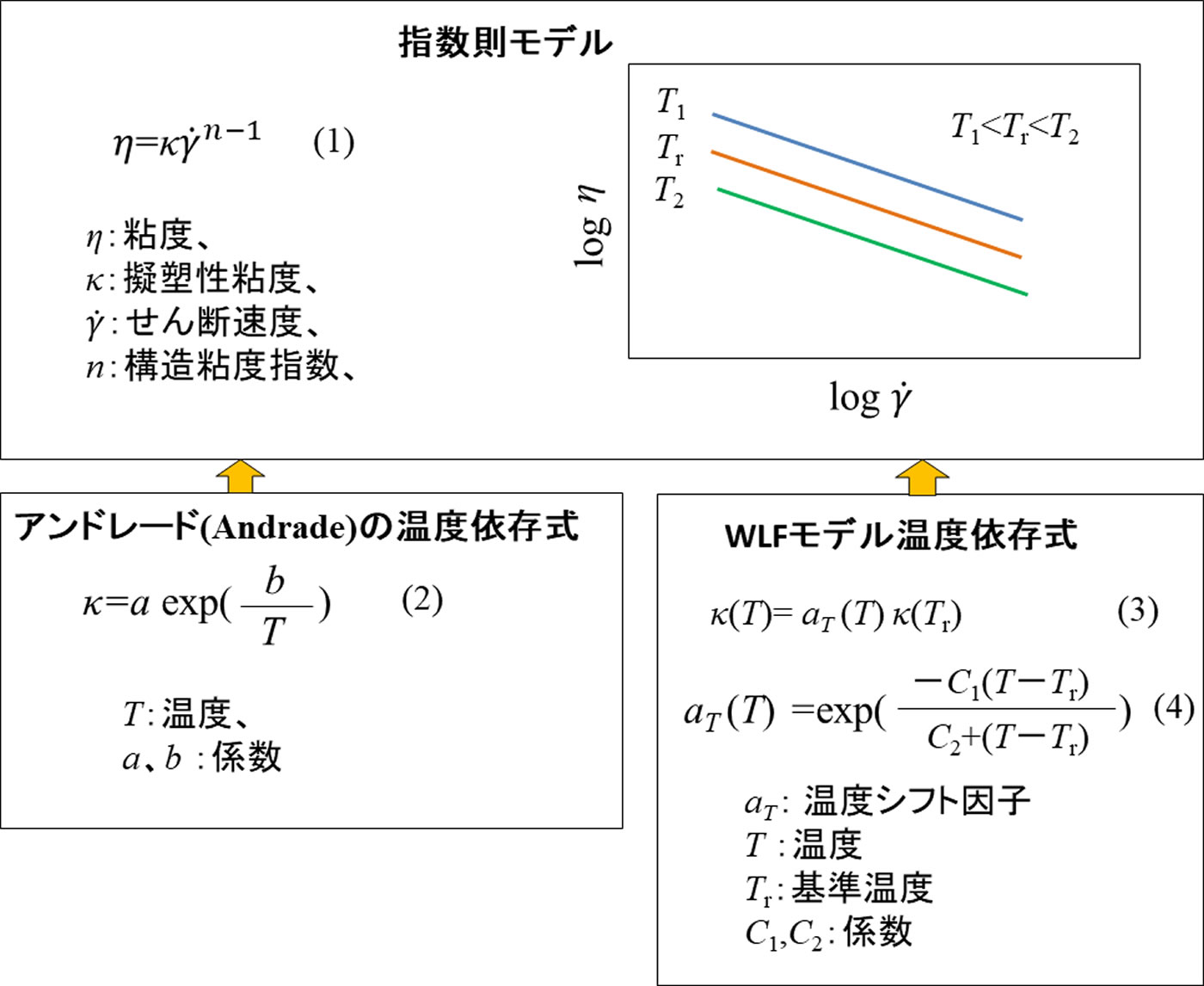
溶融樹脂の粘度は温度にも依存します。温度が高ければ粘度は低下し、低ければ粘度は増加します。図3に指数則モデルと温度依存モデルの組み合わせを示します。温度依存性モデルの代表的なものはアンドレード式とWLF式で、指数則モデルと組み合わせたとき、アンドレードの式では(2)式、WLF式では(3),(4)式の形になります。

溶融樹脂の粘度の測定は、通常せん断速度と温度の組み合わせを変えて行われます。CAEの精度確保のためには実際の粘度特性に近くなるように係数を最適化する必要があります。最適化すべき係数はアンドレードの式と組み合わせる場合は、n,a,bの三つになります。
WLFの式と組み合わせる場合は、n , \(\kappa\)(Tr),C1,C2の四つになります。

使用測定データ

非晶性エンジニアリング樹脂であるポリカ－ボネートの粘度の測定データを図4に示します。温度3水準でせん断速度を変えたときの結果です。各温度において粘度とせん断速度の両対数座標上で、せん断速度の増加とともにほぼリニアに粘度が低下しています。また、同じせん断速度では温度が高いほど粘度が低くなっています。したがって、図3に示したモデルの組み合わせが適合しています。

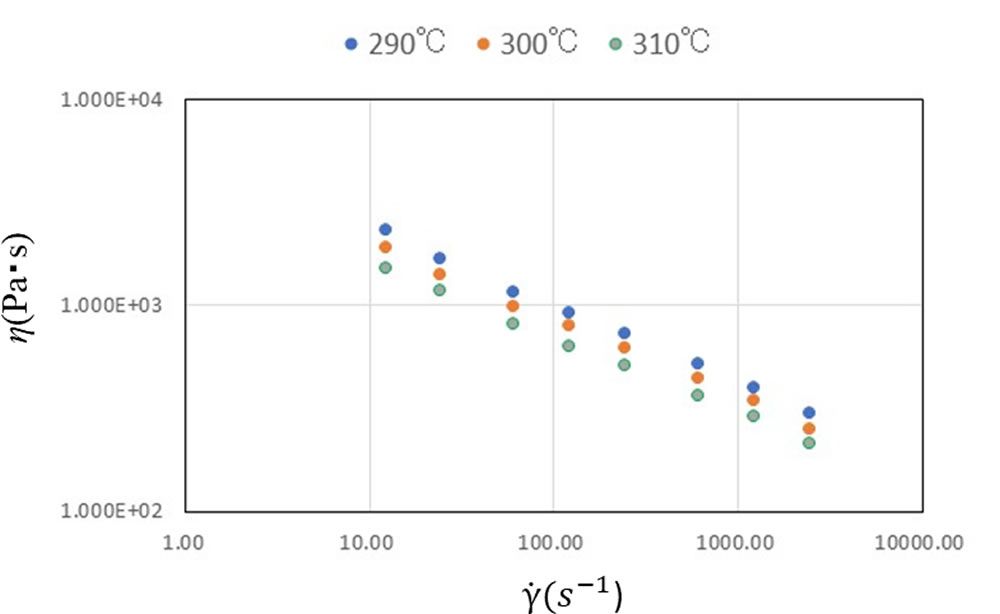
係数最適化結果

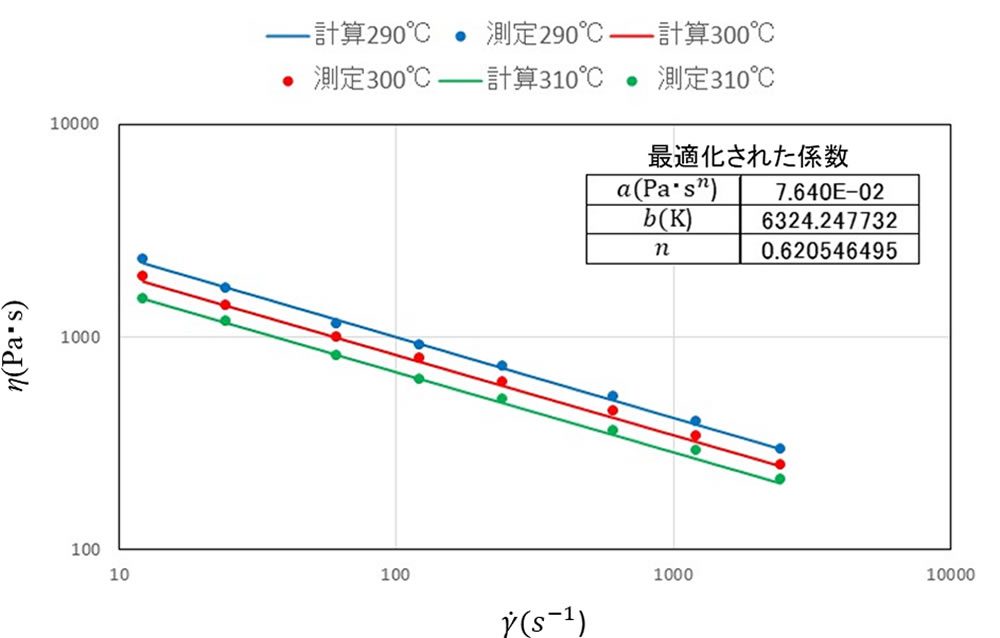
なめらかな非線形関数での最適解を求めるのに適したGRG(Generalized Reduced Gradient)非線形ソルバー¹⁾を用い、係数を最適化してみました。アンドレードの式と組み合わせたときの結果を図5に示します。計算値は測定値とよく一致しています。

参考URL:1）https://ja.helpr.me/9661-what-is-grg-nonlinear-solver

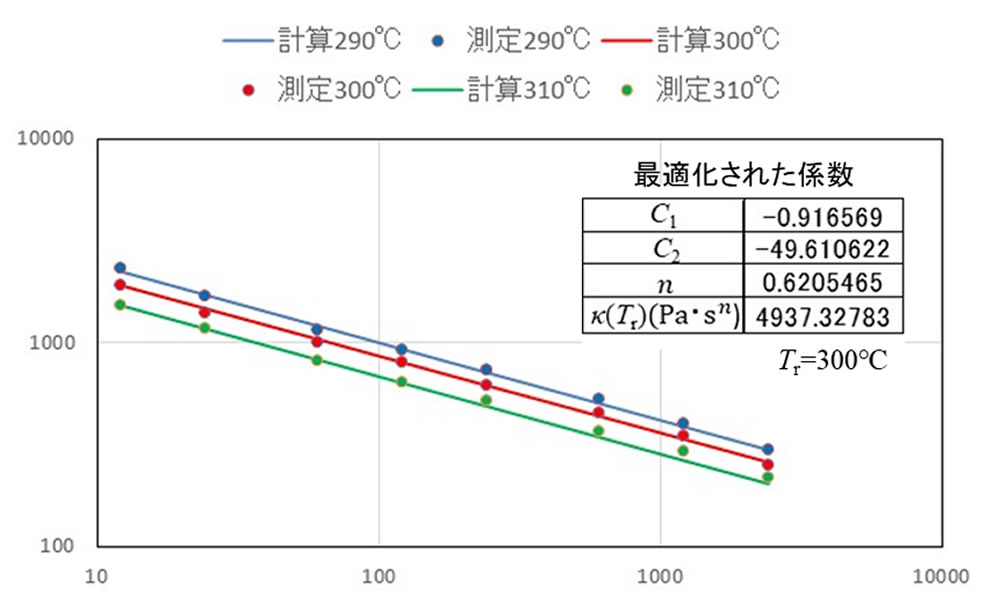
WLF式と組み合わせたときの結果を図6に示します。こちらも計算値は測定値とよく一致しています。n は温度に依存しない係数で、どちらの組み合わせでも同じ値を示しています。なお、係数が一つ多いWLFモデル使用時の方が少し誤差が小さくなりますが全体的にあまり違いはありません。

なお、Excelソルバーを用いた実材料の係数最適化手法については弊社「樹脂流体解析スキルアップセミナー」で実習できます。