樹脂成形とレオロジー第30回「Carreau（カロー）モデルの実材料への適用例」 │ DISCOVER CAE

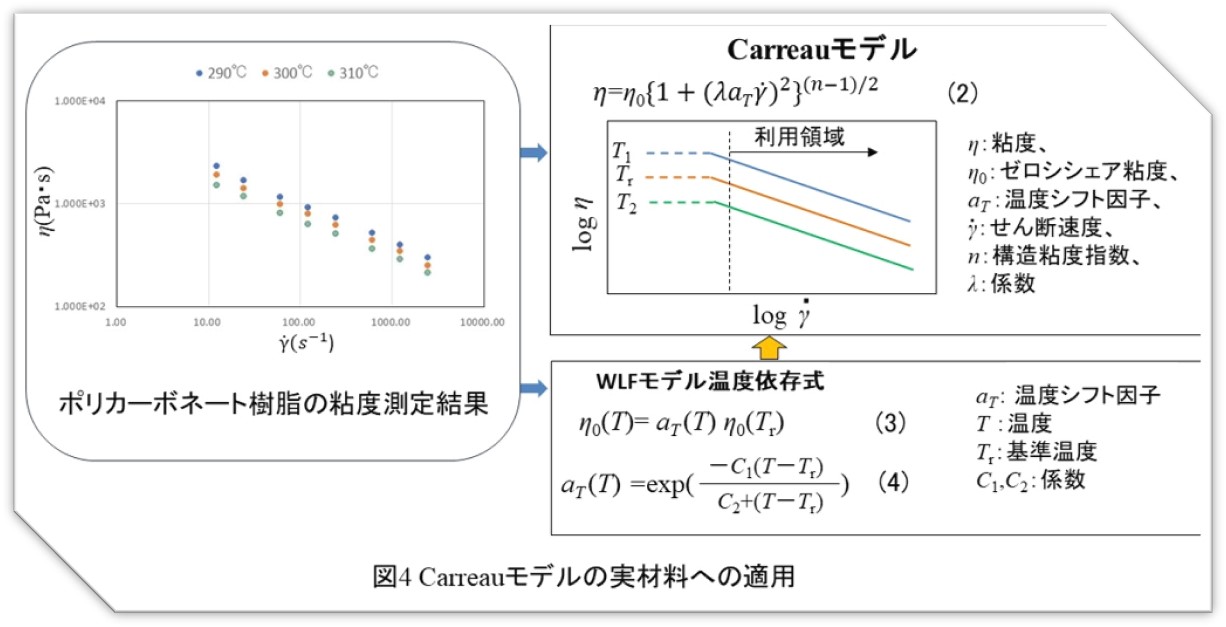
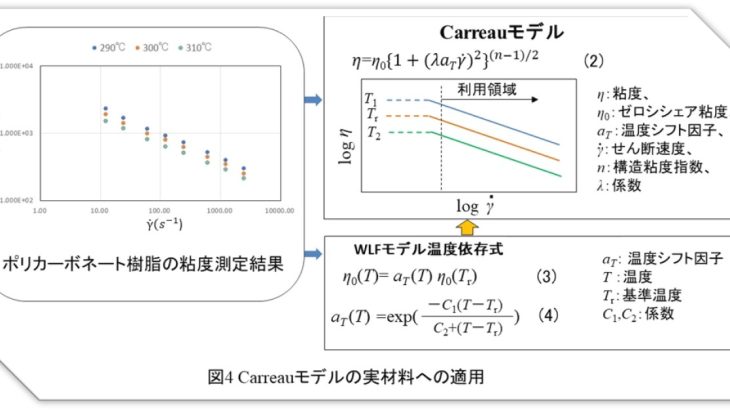
樹脂成形とレオロジー第30回「Carreau（カロー）モデルの実材料への適用例」

高分子溶融体は一般的にせん断速度が大きくなると粘度が低下する性質を持ちます。この状況を表すモデル式が色々と提案されています。ここでは、Carreauモデル¹⁾を実材料へ適用した例を示します。

Carreauモデルの特性

Carreauモデルを(1)式に示します。ここで、 \(\eta\) ：粘度、 \(\eta\)₀ ：ゼロシェア粘度、 \(\lambda\) :ニュートン流体から非ニュートン流体への遷移を表す特性時間、 \(\dot{\gamma\ }\) ：せん断速度、 n ：構造粘度指数です。

\begin{align*}\eta = \eta_0 \left\{ 1 + \left( \lambda \dot{\gamma} \right)^2 \right\}^{(n-1)/2} &\qquad ・・・・・・・(1)\end{align*}

(1)式では \(\dot{\gamma\ }\) =0で \(\eta\) = \(\eta\)₀ となります。また、n <1のとき \(\dot{\gamma\ }\) の増加とともに \(\eta\) が低下します。粘度の特性を決める係数は \(\eta\)₀ 、\(\lambda\) 、nの三つですので、二つの係数を固定したきの特性を順に調べていきます。

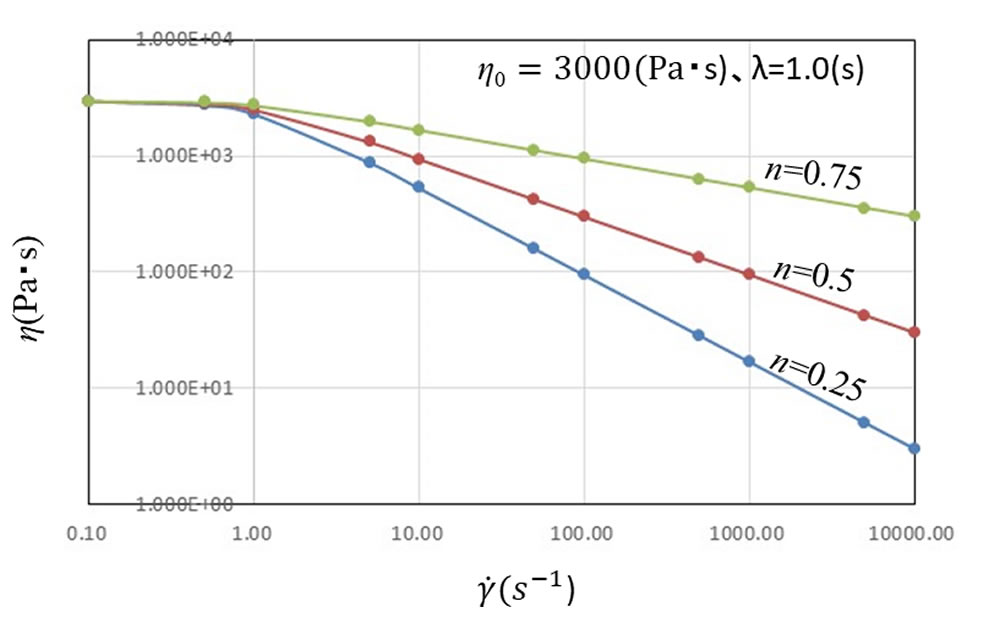
図1に \(\eta\)₀ =3000(Pa・s)、\(\lambda\) =1.0(s)に固定してnを変えたときの特性を示します。横軸は \(\dot{\gamma\ }\) 、縦軸は \(\eta\) で両対数座標上で示してあります。 \(\dot{\gamma\ }\) =0.1s^-1のところでは n によらず \(\eta\) が \(\eta\)₀ の値とほぼ一致しています。 \(\dot{\gamma\ }\) ＝1.0s^-1付近までは \(\dot{\gamma\ }\) の増加とともに \(\eta\) がゆるやかに低下し、 \(\dot{\gamma\ }\) >10sになるとほぼリニアに \(\eta\) が低下していく特性になります。また、nが小さいほど負の勾配が大きくなります。このリニアな領域は前回報告した指数則モデルと同じ役割を果たすことができます。指数則モデルでは \(\dot{\gamma\ }\) =0で発散するため、 \(\dot{\gamma\ }\) が小さいところで別途飽和粘度を設定する必要がありますが、 Carreauモデルでは最初から飽和粘度に相当する \(\eta\)₀ が設定できているため、使い勝手をよくした指数則モデルと言い換えることもできます。

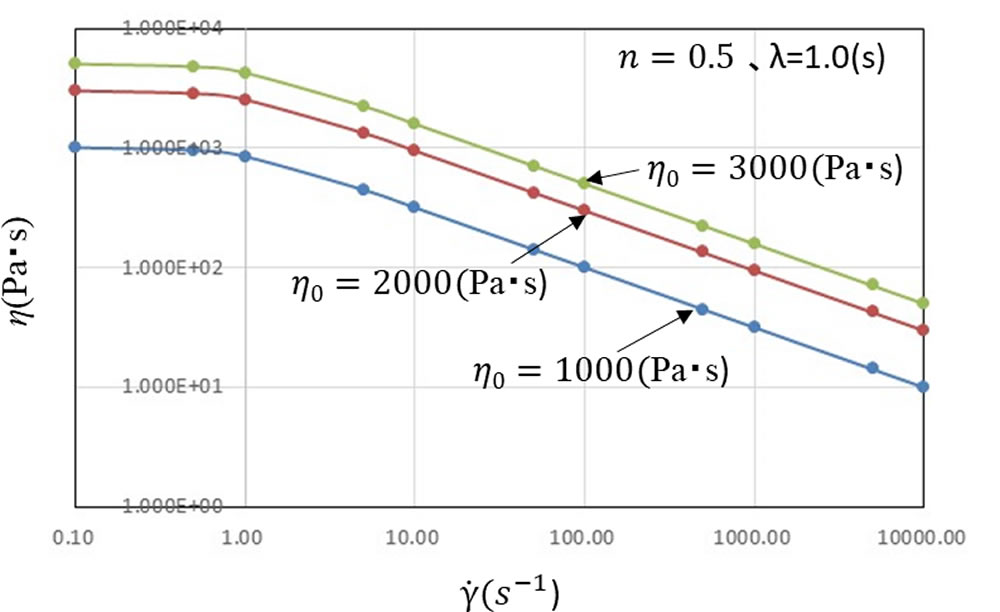
図2にn=0.5、 \(\lambda\) =1.0(s)に固定して \(\eta\)₀ を変えたときの特性を示します。 \(\eta\)₀ の増加にともない、グラフは上方に平行移動します。

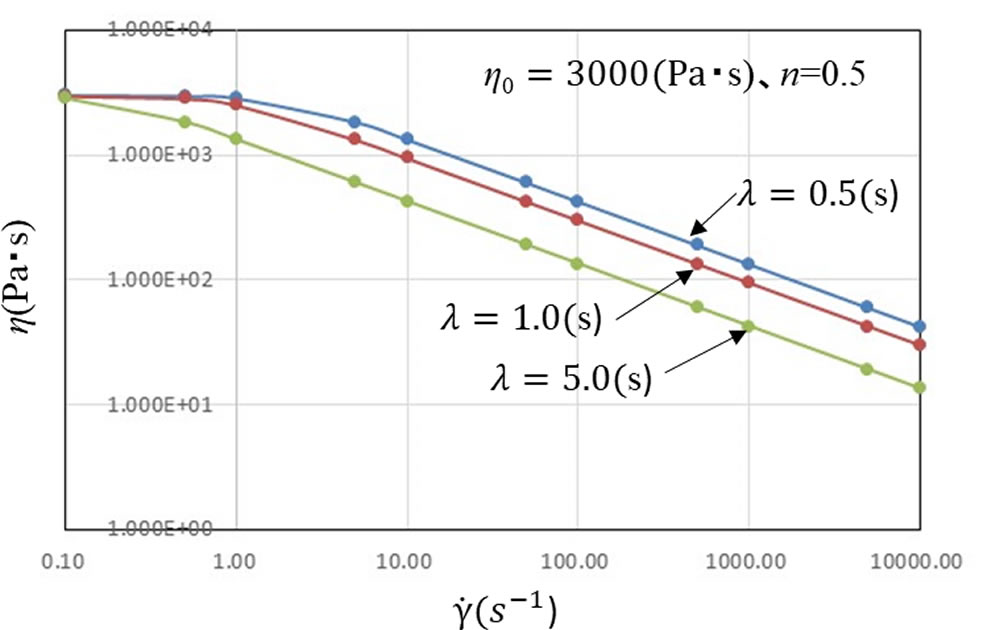
図3に\(\eta\)₀ =3000(Pa・s)、n=0.5に固定して \(\lambda\) を変えたときの特性を示します。 \(\lambda\) の増加にともない、小さい \(\dot{\gamma\ }\) で \(\eta\) が低下し始めます。 \(\eta\)₀ 、 \(\eta\) 、 n の組み合わせにより、前回指数則モデルで表した特性の樹脂もCarreauモデルに当てはめることができます。

実材料への適用

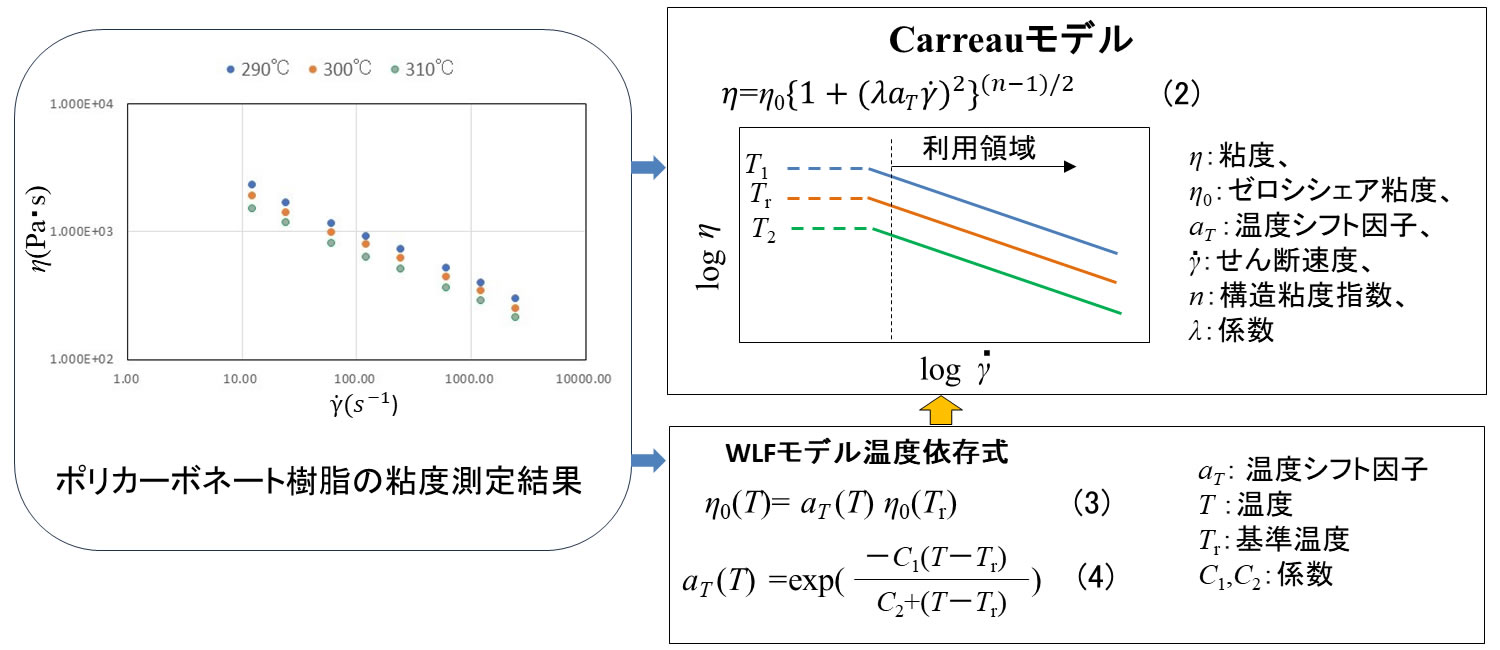
ここでは前回指数則モデルを適用したポリカーボネート樹脂をそのまま使うことにします。温度依存を考慮したときのCarreauモデルは(2)式のように温度シフト因子 a_T が加わった形になります。 a_T を使用する温度依存式はWLFモデルになります。すなわち、Carreauモデルは(3),(4)式のWLFモデルとの組み合わせで温度依存特性を表現することになります。
最適化すべき係数はn , \(\lambda\) , \(\eta\)₀(T_r),C1,C2 の五つになります。

係数最適化結果

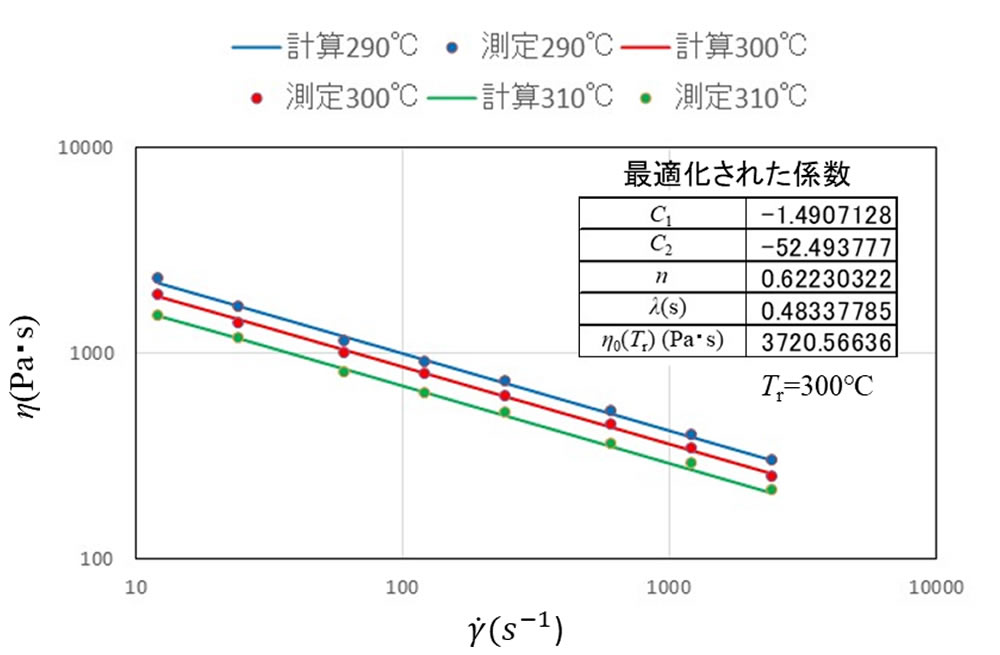
なめらかな非線形関数での最適解を求めるのに適したGRG(Generalized Reduced Gradient)非線形ソルバー²⁾を用い、係数を最適化してみました。WLF式と組み合わせたときの結果を図5に示します。計算値は測定値とよく一致しています。Carreauモデルはせん断速度が小さいときにニュートン性(粘度一定)を示し、せん断速度の増加に従い擬塑性(粘度低下)を示す材料用に考案されたものですが、指数則モデルに適合する特性の材料に対してもうまく使えることが分かりました。なお、このモデルの発展形として、高せん断速度領域で再びニュートン性を示す特性を表すBird-Carreauモデル³⁾、係数を増やしたCarreau-Yasudaモデル⁴⁾があります。 Excelソルバーを用いた実材料の係数最適化手法については弊社「樹脂流体解析スキルアップセミナー」で実習できます。

参考資料
1)牧野創、太田光浩、吉田豊、松隈洋介：SCEJ 39th Autumn Meeting ,S105(Sapporo,2007)
2)URL:https://ja.helpr.me/9661-what-is-grg-nonlinear-solver
3)米谷秀雄、北嶋英俊、松村卓美、菅貴紀、金井俊孝：成形加工19,118(2007)
4)Carreau Yasudaモデル(altair.com)