樹脂成形とレオロジー第32回「Modified Crossモデルの実材料への適用例」 │ DISCOVER CAE

樹脂成形とレオロジー第32回「Modified Crossモデルの実材料への適用例」

高分子溶融体は一般的にせん断速度が大きくなると粘度が低下する性質を持ちます。この状況を表すモデル式が色々と提案されています。ここでは、Modified Crossモデルを実材料へ適用した例を示します。

モデルの比較

Modified Cross モデルはその名の通り、前回ご報告したCrossモデルの一部を修正したものです。表1にその比較を示します。Crossモデルでは分母の括弧の外に1の数字がありますが、Modified Crossモデルでは括弧の中に1が入っています。次に同じ係数を与えて両者の特性を比較してみます。

表1のように係数を固定し、n を変えて比較してみました。

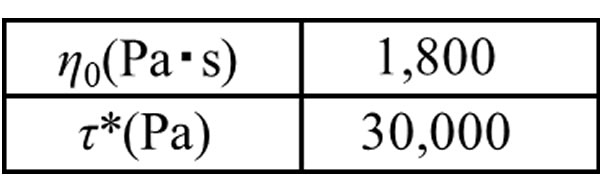
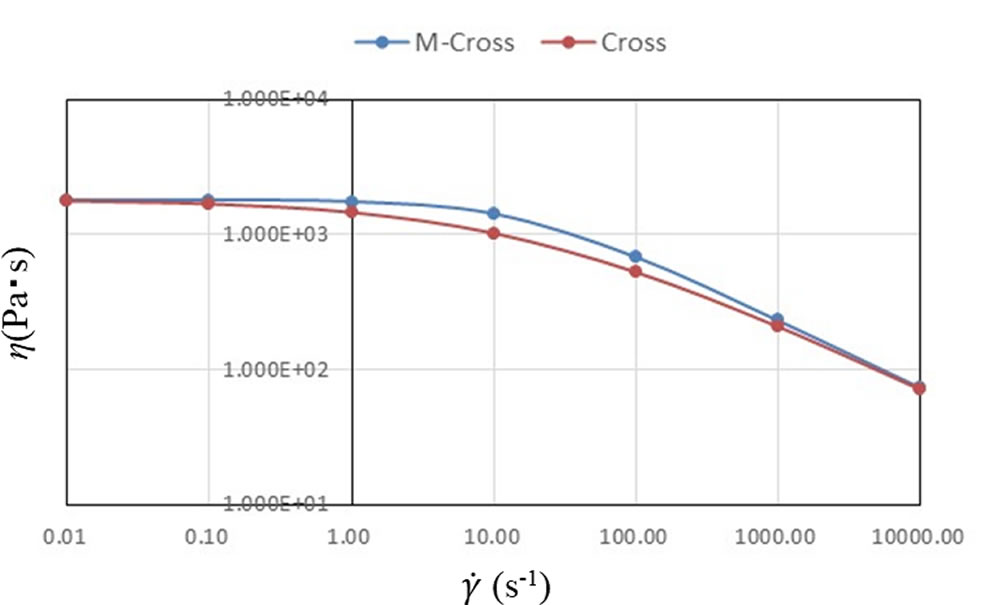
図1にn =0.5のときの特性値の比較を示します。横軸はせん断速度 \(\dot{\gamma\ }\) 、縦軸は粘度 \(\eta\) で、両対数座標軸にしてあります。このときは \(\dot{\gamma\ }\) の小さいところと大きいところで両者の値が近くなり、その間でModified Crossモデル(M-Crossと表示)の方がCrossモデルよりも値が大きくなる特性を示しています。

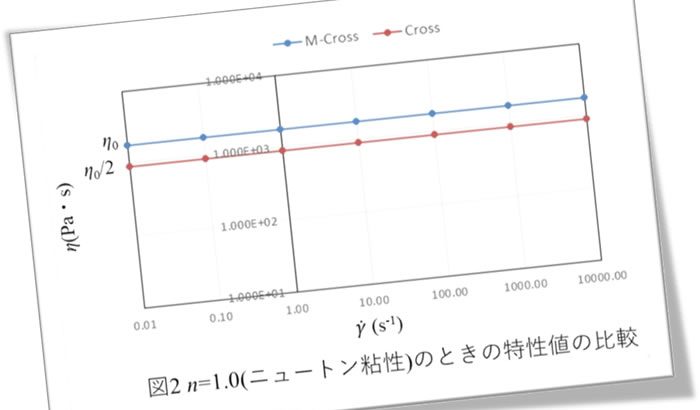
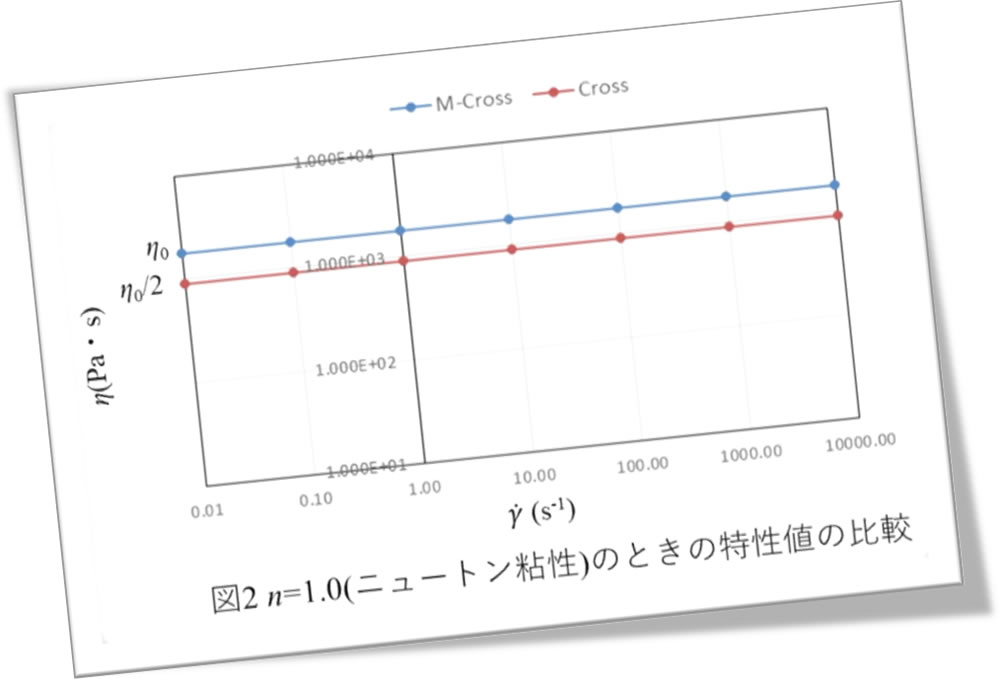
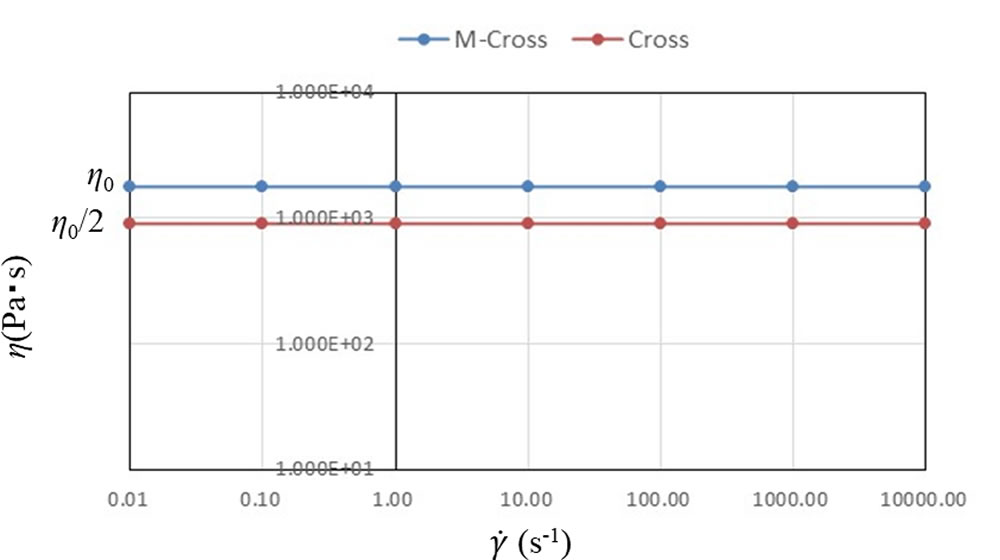
図2にn =1.0すなわち、ニュートン粘性のときの特性値の比較を示します。このとき粘度はせん断速度の影響を受けず、一定値となります。Crossモデルではこの粘度は \(\eta\)₀ の半分の値となります。一方、Modified Crossモデル(M-Cross)ではこの粘度は \(\eta\)₀ の値と一致します。すなわち、 \(\eta\)₀ にゼロシェア粘度とニュートン粘性のときの粘度という両方の意味を与えたのがModified Crossモデルになります。

実材料への適用

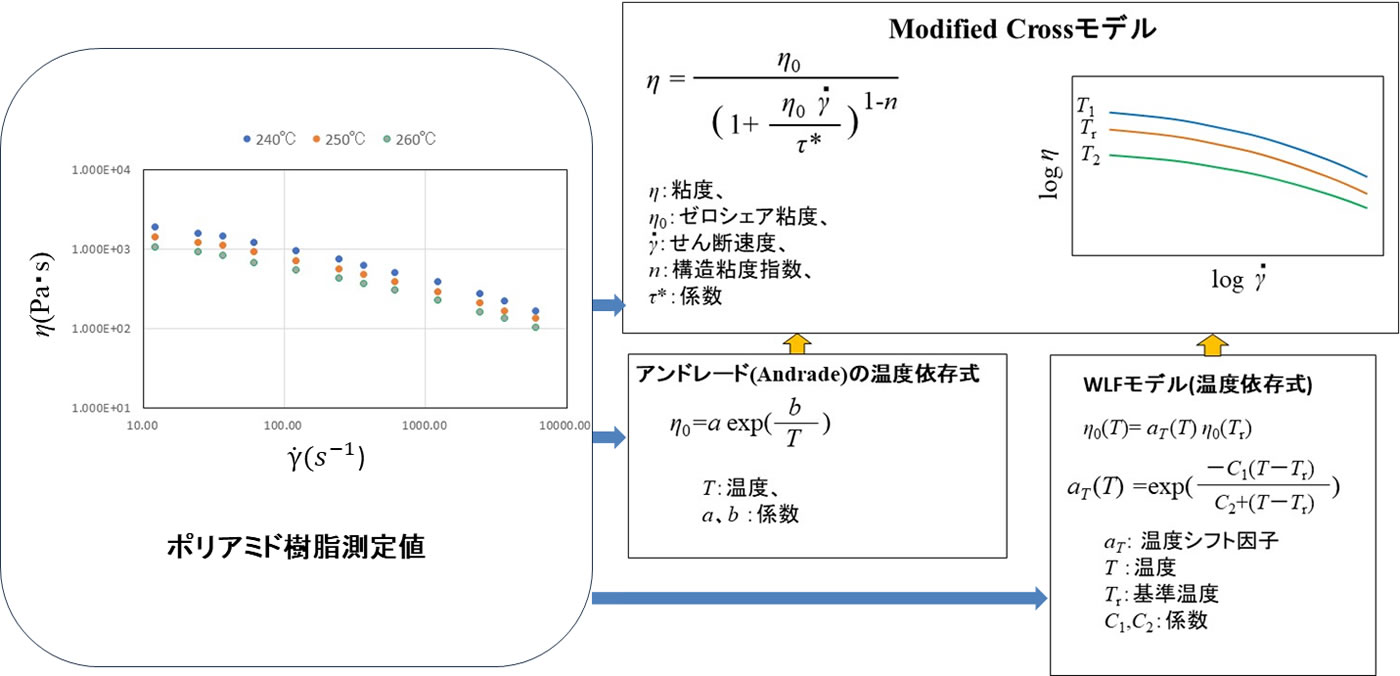
ここでは前回用いたポリアミド樹脂データを使います。図3にModified Crossモデルと温度依存モデルの実材料への適用を示します。温度依存性モデルはアンドレードの式とWLF式の二種類使い、Modified Crossモデルと組み合わせます。アンドレ－ドの式と組み合わせる場合、n , \(\tau\)^*,a,bが、WLF式と組み合わせる場合はn , \(\tau\)^*, \(\eta\)₀(T_r),C₁,C₂ が最適化すべき係数になります。

係数最適化結果

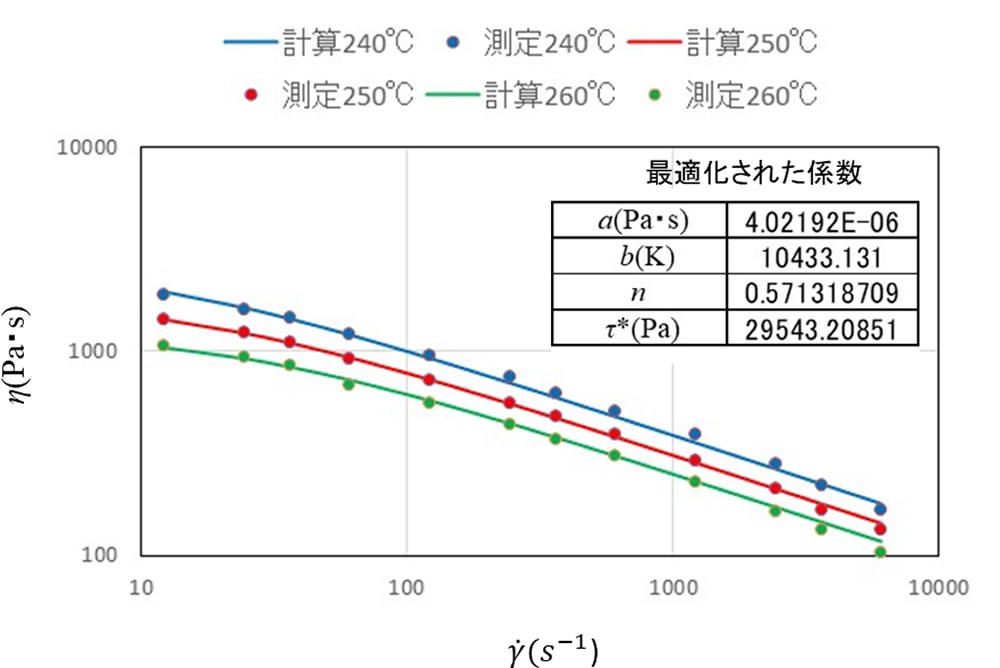
なめらかな非線形関数での最適解を求めるのに適したGRG(Generalized Reduced Gradient)非線形ソルバーを用い、係数を最適化してみました。アンドードの式と組み合わせたときの結果を図4に示します。計算値は測定値とよく一致しています。Modified CrossモデルはCrossモデルと式の形が異なりますので、最適化された係数の値もCrossモデルで示した値とは異なっています。しかし、ポリアミドのような特性を持つ材料に対しては精度良く適用できることがわかりました。

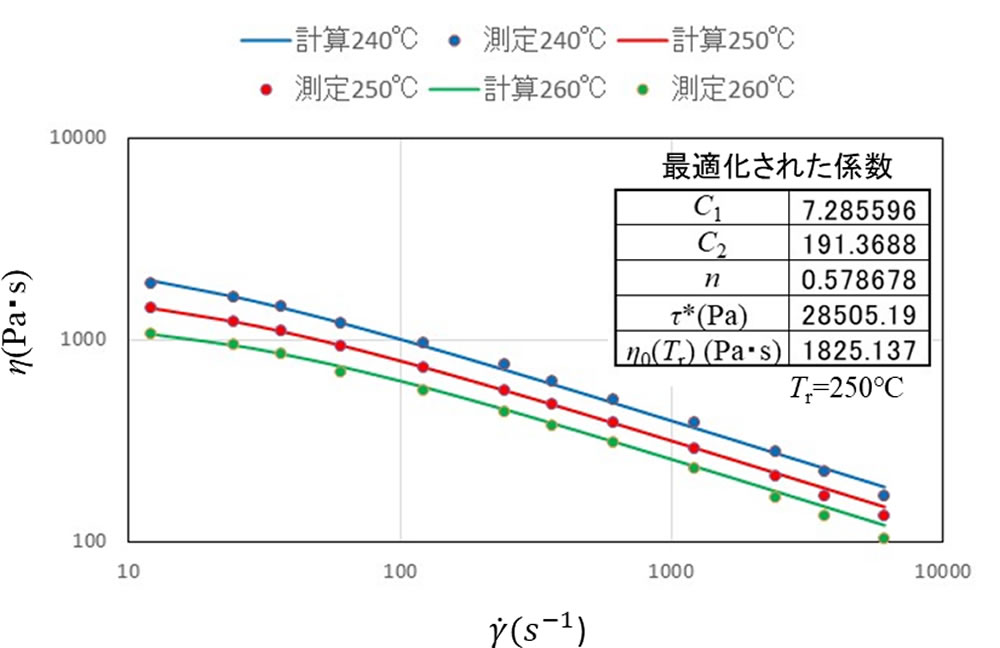
WLF式と組み合わせたときの結果を図5に示します。こちらも計算値は測定値とよく一致しています。係数が一つ多いWLFモデル使用時の方が少し誤差が小さくなりますが全体的にあまり違いはありません。 Modified CrossモデルはCrossモデルと式の形が異なりますので、最適化された係数の値もCrossモデルで示した値とは異なっています。しかし、ポリアミドのような特性を持つ材料に対しては精度良く適用できることがわかりました。

Excelソルバーを用いた実材料の係数最適化手法については弊社「樹脂流体解析スキルアップセミナー」で実習できます。