相似則を用いた準静的連成解析の高速化
プレス加工に代表される準静的現象は「慣性力が支配的にならない」との仮定の下、時間を縮めて解析する場合が有ります。これは、動的陽解法による計算を高速化するためです。しかしながら、ホットフォーミングに代表される構造-熱連成解析では、更に、冷却水の流れも考慮する構造-流体-熱連成解析では、現象時間をただ単に縮めると、解が変化してしまいます。以下では、どのようにすれば、時間を縮め、かつ、実時間で解析した場合と温度場が等価となるか、議論します。
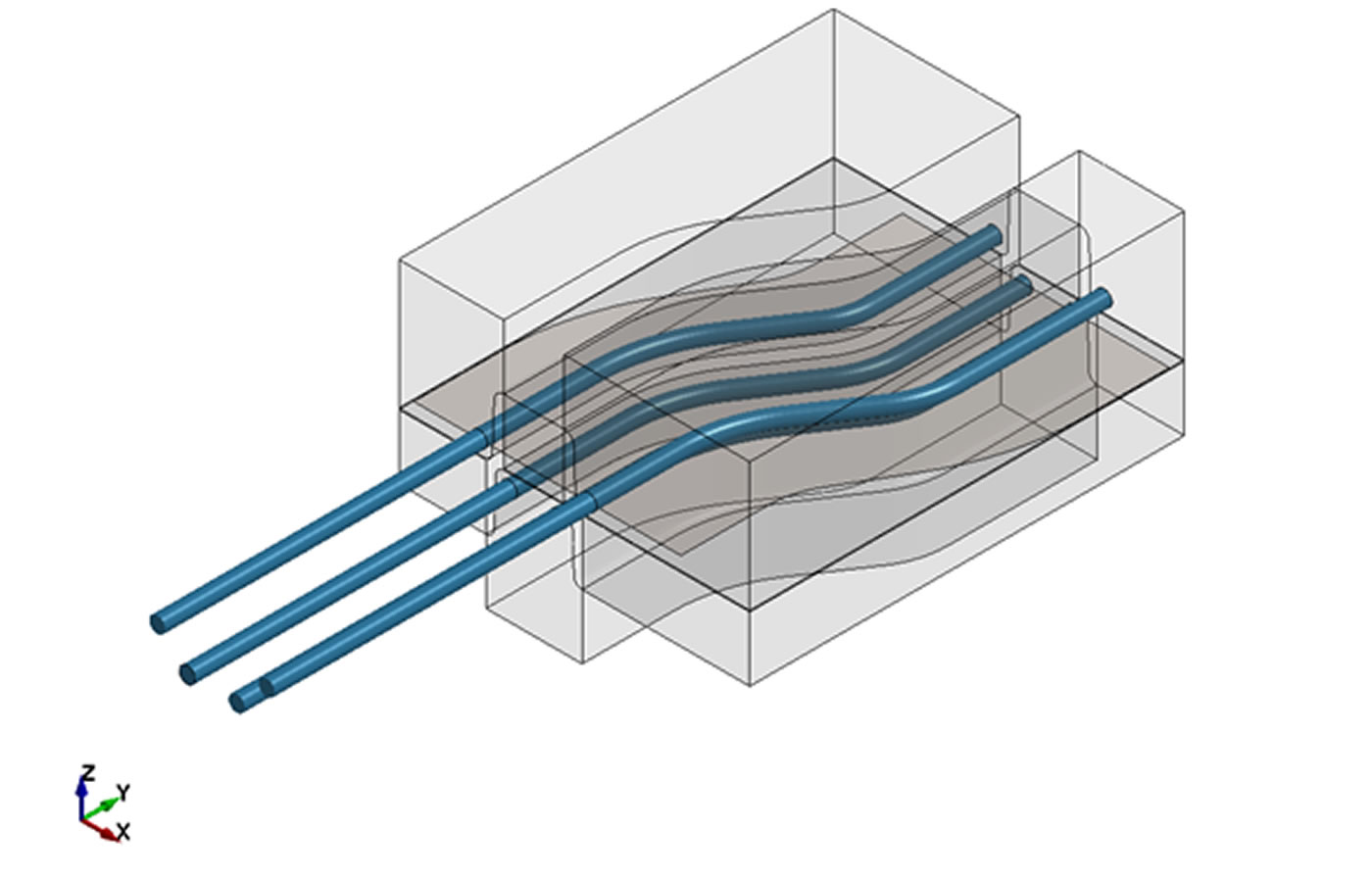
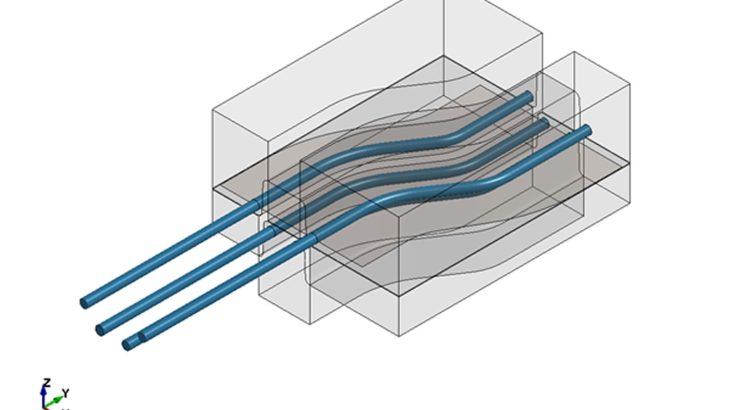
構造-流体-熱連成問題の例
ページ下部のリンクに有る「冷却水の流れを考慮したホットフォーミング解析」は、構造-流体-熱連成問題の代表例です。時々刻々拡散していく温度場を求めるため、時間を縮めると、温度場が変わってしまいます。流体の温度場も同様に、時々刻々移流・拡散するため、時間を縮めると、温度場が変わってしまいます。そのため、本解析では、各種相似則を用いて、時間を縮める代わりに入力値を工夫し、温度場を等価としています。
熱・流体の支配方程式
固体の温度場は、次式(熱伝導方程式)に支配されます。
\begin{align*}\rho C \frac{\partial T}{\partial t} = \lambda \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) + \phi 式1\end{align*}
\(\rho\):質量密度(ton/mm3)
C:比熱(mJ/ton・K)
T:温度(K)
t:時間(s)
\(\lambda\):熱伝導率(mW/mm・K)
x , y , z:座標(mm)
\(\phi\):発熱量(mW/mm3)
流体の速度場および圧力場は、次式(ナビエ・ストークス方程式と連続の式)に支配されます。(本記事では、非圧縮性流体を想定します。)
\begin{align*}&\rho \left( \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w \frac{\partial u}{\partial z} \right) = – \frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right) + f_x\\&\rho \left( \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w \frac{\partial v}{\partial z} \right) = – \frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right) + f_y 式2\\&\rho \left( \frac{\partial w}{\partial t} + u \frac{\partial w}{\partial x} + v \frac{\partial w}{\partial y} + w \frac{\partial w}{\partial z} \right) = – \frac{\partial p}{\partial z} + \mu \left( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right) + f_z\end{align*}
\begin{align*}\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 式3\end{align*}
u , v , w:x方向速度,y方向速度,z方向速度(mm/s)
p:圧力(MPa)
\(\mu\):粘性係数(MPa・s)
fx , fy , fz :x方向の体積力、y方向の体積力、z方向の体積力(N/mm3)
流体の温度場は、次式(エネルギー方程式)に支配されます。
\begin{align*}\rho C \left( \frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} + w \frac{\partial T}{\partial z} \right) = \lambda \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) + \phi 式4\end{align*}
支配方程式の無次元化
支配方程式を無次元化しておくことで、相似則が定義できます。相似則は、物理量=代表量×無次元量の形で定義されます。以下の代表量を定義し、式1~式4を無次元化することを考えます。
Tr:代表温度(K)
Lr:代表長さ(mm)
tr:代表時間(s)
\(\phi\)r:代表発熱量(mW/mm3) =\(\displaystyle \frac{\rho C T_r}{t_r}\)
Ur:代表速度(mm/s) =\(\displaystyle \frac{L_r}{t_r}\)
pr:代表圧力(mm) =\(\displaystyle \rho \left(\frac{L_r}{t_r}\right)^2\)
fr:代表体積力(N/mm3) =\(\displaystyle \frac{\rho L_r}{{t_r}^2}\)
固体の熱伝導方程式は、以下のように無次元化できます。以下で、上付き「*」は無次元化された量または式であることを表します。
\begin{align*}\frac{\partial T^*}{\partial t^*} = \frac{\color{red}{t_r \lambda}}{\rho C L_r^2} \left( \frac{\partial^2 T^*}{\partial x^{*2}} + \frac{\partial^2 T^*}{\partial y^{*2}} + \frac{\partial^2 T^*}{\partial z^{*2}} \right) + \phi^* 式1^*\end{align*}
tr \(\lambda\) /\(\rho\)CLr2 の値が等しければ、熱伝導現象は相似となります。更に、代表温度と代表長さが同じであれば、温度場は等価となります。tr \(\lambda\) が含まれることから、時間を縮める場合には、熱伝導率を高くすれば良いことが分かります。
流体のナビエ・ストークス方程式と連続の式は、以下のように無次元化できます。
\begin{align*}&\frac{\partial u^*}{\partial t^*} + u^* \frac{\partial u^*}{\partial x^*} + v^* \frac{\partial u^*}{\partial y^*} + w^* \frac{\partial u^*}{\partial z^*} = – \frac{\partial p^*}{\partial x^*} + \frac{\color{red}{\mu t_r}}{\rho L_r^2} \left( \frac{\partial^2 u^*}{\partial x^{*2}} + \frac{\partial^2 u^*}{\partial y^{*2}} + \frac{\partial^2 u^*}{\partial z^{*2}} \right) + f_x^*\\&\frac{\partial v^*}{\partial t^*} + u^* \frac{\partial v^*}{\partial x^*} + v^* \frac{\partial v^*}{\partial y^*} + w^* \frac{\partial v^*}{\partial z^*} = – \frac{\partial p^*}{\partial y^*} + \frac{\color{red}{\mu t_r}}{\rho L_r^2} \left( \frac{\partial^2 v^*}{\partial x^{*2}} + \frac{\partial^2 v^*}{\partial y^{*2}} + \frac{\partial^2 v^*}{\partial z^{*2}} \right) + f_y^* 式2^*\\&\frac{\partial w^*}{\partial t^*} + u^* \frac{\partial w^*}{\partial x^*} + v^* \frac{\partial w^*}{\partial y^*} + w^* \frac{\partial w^*}{\partial z^*} = – \frac{\partial p^*}{\partial z^*} + \frac{\color{red}{\mu t_r}}{\rho L_r^2} \left( \frac{\partial^2 w^*}{\partial x^{*2}} + \frac{\partial^2 w^*}{\partial y^{*2}} + \frac{\partial^2 w^*}{\partial z^{*2}} \right) + f_z^*\end{align*}
\begin{align*}\frac{\partial u^*}{\partial x^*} + \frac{\partial v^*}{\partial y^*} + \frac{\partial w^*}{\partial z^*} = 0 式3^*\end{align*}
\(\mu\)tr /\(\rho\)CLr2 (1/レイノルズ数)の値が等しければ、速度場および圧力場は相似となります。更に、代表長さが同じであれば、流れのパターン(流線等)は等価となります。\(\mu\)tr が含まれることから、時間を縮める場合には、粘性係数を高くすれば良いことが分かります。
流体のエネルギー方程式は、以下のように無次元化できます。
\begin{align*}\frac{\partial T^*}{\partial t^*} + u^* \frac{\partial T^*}{\partial x^*} + v^* \frac{\partial T^*}{\partial y^*} + w^* \frac{\partial T^*}{\partial z^*} = \frac{\color{red}{t_r \lambda}}{\rho C L_r^2} \left( \frac{\partial^2 T^*}{\partial x^{*2}} + \frac{\partial^2 T^*}{\partial y^{*2}} + \frac{\partial^2 T^*}{\partial z^{*2}} \right) + \phi^* 式4^*\end{align*}
tr \(\lambda\)/\(\rho\)CLr2 の値が等しければ、熱伝導現象は相似となります。更に、代表温度と代表長さが同じであれば、温度場は等価となります。tr \(\lambda\)が含まれることから、時間を縮める場合には、熱伝導率を高くすれば良いことが分かります。
冷却水の流れを考慮したホットフォーミング解析における入力値の工夫
事例では、上記の考察から、入力値を以下のように工夫しました。
1. 代表時間を現象時間とし、時間を縮める。
実時間:23s
→解析上の時間:0.17037s(1.0/135.0倍)
2. 固体・流体共、tr \(\lambda\)を変えないよう熱伝導率をスケーリング。
固体の熱伝導率:32.0 mW/mm・K
→解析入力値:4320 mW/mm・K(135.0倍)
流体の熱伝導率:0.6104 mW/mm・K
→解析入力値:82.404 mW/mm・K(135.0倍)
3. 流体について、\(\mu\)tr を変えないよう、粘性係数をスケーリング。
流体の粘性係数:8.544×10-10 MPa・s
→解析入力値:1.15344×10-7 MPa・s(135.0倍)
まとめ
固体の準静的解析において、熱・流体との連成が有る場合には、相似則を用いて等価な温度場が得られることを示しました。
※別途、熱伝達境界・輻射境界・接触熱伝達境界の無次元化が必要ですが、本記事では割愛します。
※本例では、時間を縮めたことにより、流体の速度場・圧力場・体積力場は相似則を満たすように変化します。従って、金型のたわみ等、流体力を受けて構造側が変形するような問題には、本手法は適用できません。
※工具の加速・減速により、一時的に、流体の体積力が無視できなくなりますが、工具のストローク速度は一定の時間が大半を占めるため、大半の時間において、速度場のパターンは、高速化しない場合と同じになります。
関連ページ
●冷却水の流れを考慮したホットフォーミング解析
※本記事で議論した手法を用いて解析しています。