樹脂成形とレオロジー第33回「ビンガム塑性流体」
通常の流体はせん断応力が加わるとそれに応じた速度で動き出します。しかし、所定の応力に達するまでは動くことができず、その応力を超えると流動を開始する物質も存在します。流動開始に必要な応力を降伏応力といいます。また、このような流れを塑性流動といいます。練り歯磨き、石鹸、バターなどの身近な材料がこれに該当します。ここでは塑性流動を生じる代表例としてビンガム塑性流体1)を取り上げて特性を説明していきます。
ビンガム塑性流体の特性
構成方程式は(1)～(3)式になります。
\begin{align*}\tau < \tau_0 &\quad \text{で} \quad \dot{\gamma} = 0 \qquad \qquad ・・・・・・・(1)\end{align*} \begin{align*}\tau \geq \tau_0 &\quad \text{で} \quad \tau = \tau_0 + \eta_N \dot{\gamma} \qquad \qquad ・・・・・・・(2)\end{align*} \begin{align*}\tau &= \eta \dot{\gamma} \qquad \qquad ・・・・・・・(3)\end{align*} \(\tau\) ：せん断応力 \(\tau\)0 ：降伏応力 \(\dot{\gamma\ }\) ：せん断速度 \(\eta\)N :ニュートン粘度 \(\eta\) ：粘度
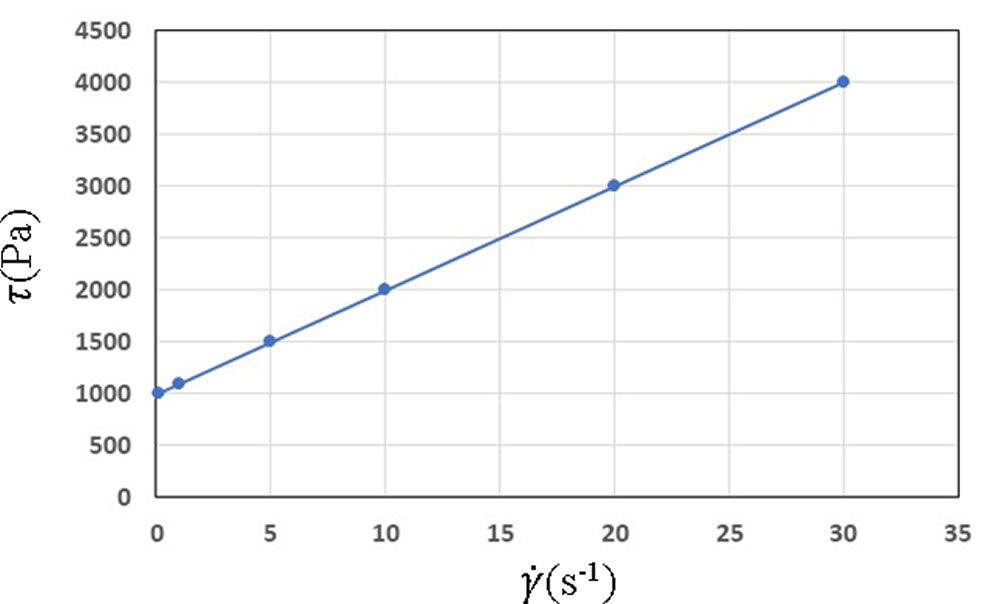
ここで、表1のように \(\tau\)0 と \(\eta\)N を固定して \(\tau\) と \(\dot{\gamma\ }\) の関係を調べてみます。これを図1に示します。\(\tau\) が \(\tau\)0 に達するまでは流動しませんので、せん断速度は生じず \(\dot{\gamma\ }\) =0のままです。\(\tau\) = \(\tau\)0 になると流動を開始し、\(\dot{\gamma\ }\) に比例して \(\tau\) が増加します。この領域での勾配がニュートン粘度 \(\eta\)N となります。すなわち、ビンガム流体とはニュートン流体に \(\tau\)0 を上乗せした特性になります。
(2)式と(3)式により次式が導かれます。
\begin{align*}\eta = \frac{\tau_0}{\dot{\gamma}} + \eta_N &\qquad ・・・・・・・(4)\end{align*}
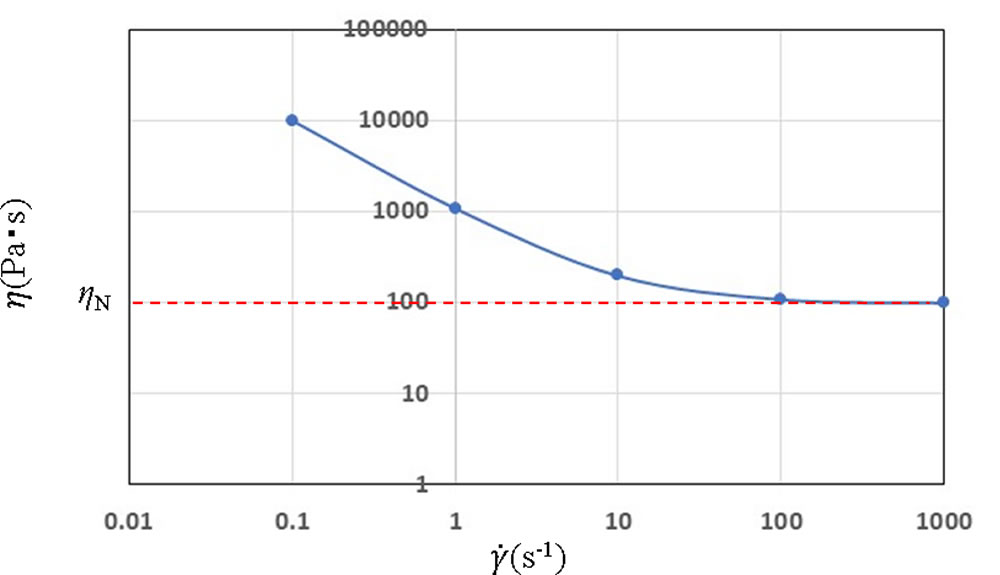
表1と同じ係数を与えたときの(4)式の特性は図2のようになります。\(\eta\) と \(\dot{\gamma\ }\) は反比例の関係となり、\(\eta\) は \(\dot{\gamma\ }\) の増加とともに\(\eta\)N に漸近していきます。粘度の測定で図2のような形が得られたら、ビンガム塑性流体とみなすことができます。
Excelソルバーを用いた実材料の係数最適化手法については「樹脂流体解析スキルアップセミナー」で実習できます。
ビンガム塑性流体の円管内の流動解析
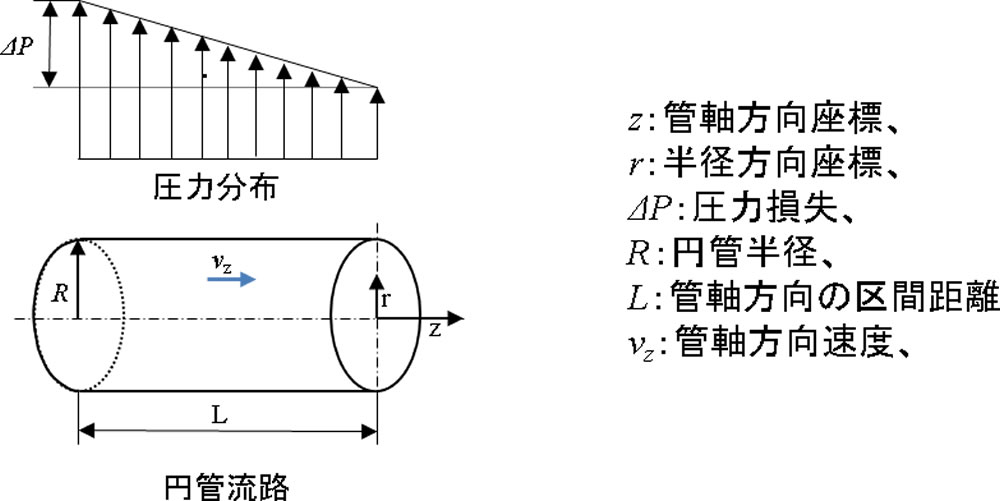
いま、同じ半径の一本の円管内を等温の非圧縮性ビンガム流体が満たし、定常層流で管軸方向のみに流動し、管壁ですべりがなく、重力などの体積力が働かないと仮定します。円管流路諸元と流動時に生じる物理量の一部を図3に示します。
(2)式を書き換えると次式になります。
\begin{align*}\dot{\gamma} &= \frac{\tau}{\eta_N} – \frac{\tau_0}{\eta_N} &\qquad ・・・・・・・(5)\end{align*}
図3の流動状態での運動方程式から次式が得られます。
\begin{align*} \dot{\gamma} &= \frac{\partial v_z}{\partial r} \qquad ・・・・・・・(6) \\ \tau &= \frac{r \Delta P}{2L} \qquad ・・・・・・・(7) \end{align*}
(6)、(7)式を(5)式に代入すると次式になります。
\begin{align*}\frac{\partial v_z}{\partial r} &= \frac{r \Delta P}{2 \eta_N L} – \frac{\tau_0}{\eta_N} &\qquad ・・・・・・・(8)\end{align*}
せん断速度が0になる位置のrをr*とすると上式で左辺を0とおいて次式が得られます。
\begin{align*}r^* &= \frac{2 \tau_0 L}{\Delta P} &\qquad ・・・・・・・(9)\end{align*}
r*より内側の領域では速度は一定になり、外側の領域では速度分布を生じます。
(8)式を境界条件(r =Rでvz =0)を用いて積分すると次の速度式が得られます。
\begin{align*}v_z &= -\frac{R^2 \Delta P}{4 \eta_N L} \left( 1 – \left( \frac{r}{R} \right)^2 \right) + \frac{R \tau_0}{\eta_N} \left( 1 – \frac{r}{R} \right) &\qquad ・・・・・・・(10)\end{align*}
この式はr*≦r≦Rの領域に適用されます。r≦r*の領域では次の一定流速の式になります。
\begin{align*}v_z &= -\frac{R^2 \Delta P}{4 \eta_N L} \left( 1 – \left( \frac{r^*}{R} \right)^2 \right) + \frac{R \tau_0}{\eta_N} \left( 1 – \frac{r^*}{R} \right) &\qquad ・・・・・・・(11)\end{align*}
ここで表2のように値を与えて速度分布の計算を行いました。
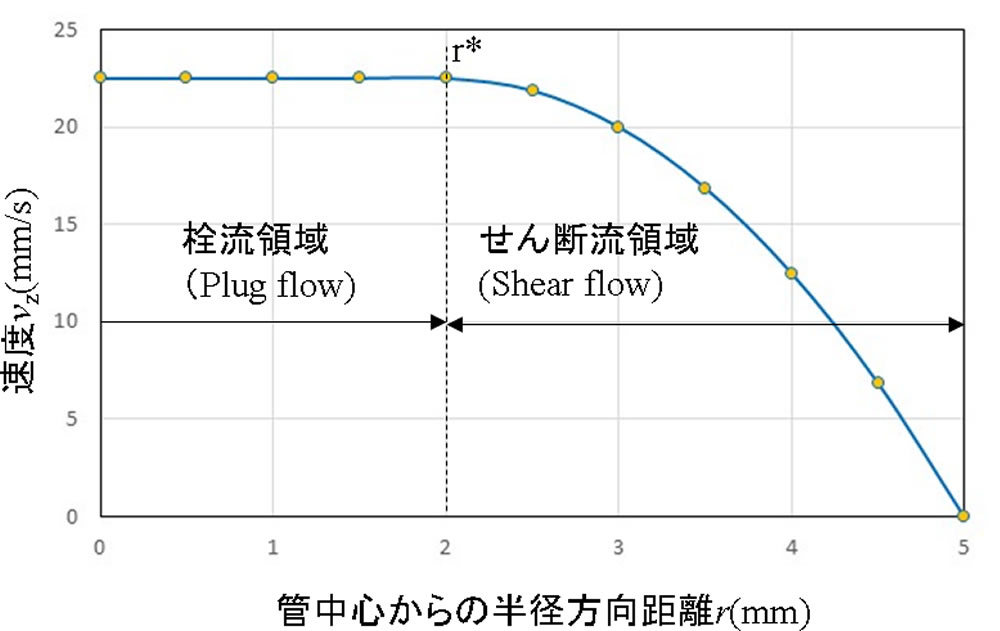
図4にビンガム塑性流体の速度分布の例を示します。横軸は管中心からの半径方向距離r 、縦軸は速度vzです。圧力勾配と逆方向に流動するため(10)式の速度は負号が付きますが、ここでは正の値に変えています。管中心から2mmの距離のところがr* であり、それより内側が速度一定の栓流(Plug flow)領域、外側がせん断流(Shear flow)領域になっています。塑性流動をする材料はこのような特異な流動プロファイルを持ちます。
なお、ビンガム塑性流体はレオロジーという学問分野の提唱者であるEugene Cook Binghamの名を冠して付けられたものです。この流体の係数最適化手法については弊社「樹脂流体解析スキルアップセミナー」で実習できます。
参考文献：1) J.M.Mackelvey,”Polymer Processing“,p71 Jon Wiley and Sons,Inc. New York(1962)
関連記事/関連ページ